[科普中国]-哈密顿量

简介

在量子力学中，在大多数情况下，哈密顿量是对应于系统的总能量的运算符。 它通常由H表示，也称为Ȟ或Ĥ。 其频谱是衡量系统总能量时可能产生的结果。 由于它与系统的时间演化密切相关，所以在量子理论的大多数形式中是至关重要的。

哈密尔顿人以威廉·罗文·汉密尔顿（William Rowan Hamilton）命名，他也创造了牛顿力学的革命性改革，现在称为哈米尔顿力学，这在量子物理学中是重要的。

哈密顿量是所有粒子的动能的总和加上与系统相关的粒子的势能。 对于不同的情况或数量的粒子，哈密顿量是不同的，因为它包括粒子的动能之和以及对应于这种情况的势能函数。1

薛定谔哈密尔顿一个粒子通过与经典力学类似，哈密顿量通常表示为对应于系统的动能和势能的运算符的总和。

H=T+V（其中T是动能，V是势能）。

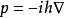是动量算子，其中∇是del运算符。 ∇自身的点积是拉普拉斯算子∇2。

虽然这不是经典力学中哈密顿量的技术定义，但它是最常见的形式。 将这些组合在一起产生在Schrödinger方程中使用的熟悉形式：

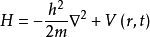
这允许将哈密顿量应用于由波函数Ψ（r，t）描述的系统。 这是采用Schrödinger波浪力学形式学的量子力学介绍性处理方法。

人们还可以对某些变量进行替换以适应特定情况，例如涉及电磁场的一些变量。2

许多粒子由于势能取决于颗粒的空间排列，动能也将取决于空间配置以节省能量。 由于任何一个粒子的运动将由于系统中所有其它粒子的运动而变化。 为此，动能的交点可能出现在哈密尔顿算子中; 混合两个颗粒的梯度：

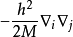
其中M表示导致该额外动能的颗粒的集合的质量。 这种形式的术语称为质量极化项，并且出现在许多电子原子的哈密尔顿（见下文）。

对于N相互作用的粒子，即相互作用并构成多体情况的粒子，势能函数V不仅仅是分开的电位（并且当然不是产品，因为它在尺寸上不正确）的总和。 势能函数只能如上所述：每个粒子的所有空间位置的函数。

对于不相互作用的颗粒，即不相互作用并独立移动的颗粒，系统的电位是每个颗粒的单独势能的总和，即

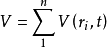
在这种情况下，哈密顿量的一般形式是：

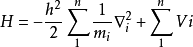
其中所有颗粒的总和及其相应的电位；结果是系统的哈密尔顿算子是每个粒子的单独哈密尔顿算子的总和。 这是一个理想的情况 - 在实践中，粒子通常总是受到一些潜在的影响，并且有许多身体的相互作用。 这种形式不适用的两体互动的一个说明性实例是由于带电粒子引起的静电势，因为它们通过库仑相互作用（静电力）彼此相互作用，如下所示。

哈密尔顿方程经典哈密顿力学中汉密尔顿方程在量子力学中有直接的类比。 假设我们有一组基本状态n，这不一定是本能状态的能量。为了简单起见，我们假设它们是离散的，并且它们是正交的，我们将假设哈密尔顿算子也是独立于时间的。34

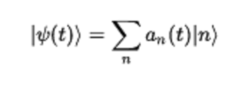
系数a（t）是复数变量。 我们可以将它们视为指定系统状态的坐标，例如指定经典系统的位置和动量坐标。 像古典坐标一样，它们通常不是时间常数，它们的时间依赖性导致整个系统的时间依赖性。

这个状态的哈密顿量的期望值也是平均能量

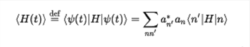
每个an（t）实际上对应于两个独立的自由度，因为变量具有实部和虚部。 我们现在执行以下技巧：不使用实部和虚部作为独立变量，我们使用（t）及其复共轭a *（t）。 通过这种自变量的选择，我们可以计算偏导数,那么上面的方程就变成了

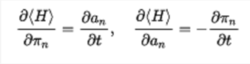
这正是哈密顿方程的形式。

其他信息===================================================================================

所谓哈密顿量的对角化就是解一个本征值问题(在线性代数中就是特征值和特征向量)。对角化哈密顿量的过程就是一个找能量本征值的过程（找到这个系统可能存在的能量）。或者是一个去耦合的过程（比如说两个弹簧振子振动时存在耦合，可以写成一个哈密顿量的形式，对角化后，找到了弹簧振子的简振模，就去耦合了）

对角化的物理含义就是找到一个能量系统中的可能能量（一般来说这些能量都是分立的，这就是量子力学的精髓之一）

在势场V（x）中的粒子，其经典哈密顿量H=T+V的算符表示成 Hamilton算符=动能算符+势能，势能是与位置X相关的量，没有相应的算符表示，而动能算符表示为 （动量算符的平方/两倍的质量）。 动量算符的表达形式在计算自由粒子动量平均值的过程中通过自由粒子在坐标和动量表象下的波函数变换求出。具体的公式推导可以去看量子力学。

薛定谔方程的表达形式就是哈密顿量本征函数的形式。