简介
伯格斯方程(Burgers equation) 是一个模拟冲击波的传播和反射的非线性偏微分方程。12
伯格斯方程是应用数学的各个领域的基本偏微分方程,如流体力学,非线性声学,气体动力学。 它被用约翰内斯·马丁斯汉堡(1895-1981)的名字命名。
对于给定的字段y(x,t)和扩散系数(或粘度,如在原始流体力学上下文中)d,伯格斯方程也称为粘性伯格斯方程)在一个空间维度是耗散系统:
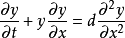
增加时空噪声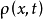 形成随机伯格斯方程3
形成随机伯格斯方程3
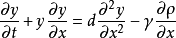
伯格斯方程只适用于一个空间维度,Kardar-Parisi-Zhang方程则广泛应用于多个维度。
当扩散项不存在(即d = 0)时,伯格斯方程成为不粘伯格斯方程:
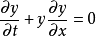
这是可以发展不连续性(冲击波)的守恒方程的原型。 以前的方程式是伯格斯方程的“平流形式”。 “保护形式”是
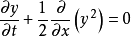
求解不含伯格斯的方程;
无粘连的伯格斯方程是一个守恒方程,更一般地说是一阶准线性双曲线方程。 事实上,通过将其电流密度定义为动能密度:
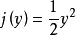
它可以放入电流密度均匀的形式:
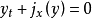
保守方程的解可以通过特征方法构建。 该方法产生如果X(t)是普通微分方程的解:
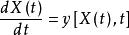
结论: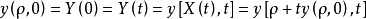 ,这是一个隐含的关系,决定了不含相关伯格斯方程式的解。 如果特征相交,则不存在PDE的经典解决方案。
,这是一个隐含的关系,决定了不含相关伯格斯方程式的解。 如果特征相交,则不存在PDE的经典解决方案。
粘性伯格斯方程4:
粘性伯格斯方程可以通过Cole-Hopf变换线性化。
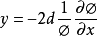
将其转化为方程式,可以将其与x相集成,
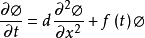
其中f(t)是取决于边界条件的函数。 如果f(t)= 0相同(例如,如果问题要在周期性域上解决),那么我们得到扩散方程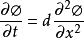 。
。
扩散方程可以解决,Cole-Hopf变换反演,得到伯格斯方程的解:
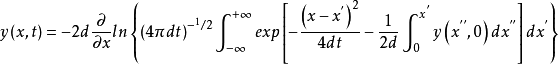




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国