[科普中国]-正则方程

方程简介

经典力学中一组描写系统运动的一阶微分方程组。是W.R.哈密顿于1834年提出的，又称哈密顿方程或正则方程。可写为：

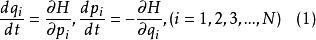
（1）式中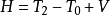 ，称为哈密顿函数，T2和T0分别为动能T中用广义坐标表示的二次齐次式和零次齐次式（即不含p，仅含q和t之式），V为用广义坐标表示的势能函数。

对于定常系统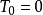 ， ，则H=T+V，即这种力学系统的哈密顿函数就是这系统用广义动量和广义坐标表示的机械能。1

由于H函数须将T中的q换成p，所以求正则方程要比求拉格朗日方程多一层运算手续。正则方程是2N个一阶微分方程组；拉格朗日方程是N个2阶微分方程组。正则方程形式上的优点是每一式只有一个导数，而且在式（1）的左边，右边是q，p，t的函数。若令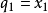 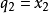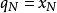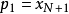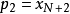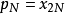， ，…， ； ， ，…， ，则式（1）可写成：

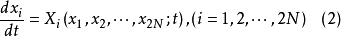
这种微分方程在数学中有系统的研究。234

力法正则方程以多余约束力作为基本未知量、由变形谐调条件建立补充方程求解超静定问题的方法称为力法。

用力法求解超静定系统需遵循以下步骤：①判断多余约束的个数，即确定超静定的阶数；②解除所有的多余约束选择原超静定结构的一个静定基；③施加外载荷和多余约束力以及对应的约束条件，形成一个相当系统；④在相当系统上列出求解约束位移的补充方程(组)，补充方程中包含有未知的多余约束力；⑤求解补充方程中的未知数即多余约束力。

从上述求解步骤可以看出，在相当系统上列出包含有未知多余约束力的补充方程(组)是一个关键环节。在解除多余约束代之以多余约束的同时，多余约束在其作用点对超静定系统的位移的限制与多余约束力的作用方向正好相反(如限制向下的线位移则多余约束力向上、限制逆针向转动的约束力偶必须顺针向等)，也就是说，多余约束与对应的约束位移之间一定是一对广义力与广义位移的关系，由此可以得到求解超静定问题的正则方程。

设一个n阶超静定结构的n个多余约束力为Xi，(i=1~n)，对应的约束位移为Δi。在相当系统上还有外载荷，外载荷在Xi作用点引起的与Xi对应的广义位移为ΔiF，多余约束力Xj在Xi作用点引起的广义位移为Δij，根据位移叠加法

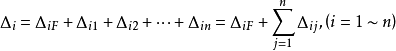
因为Δij是Xj单独作用在相当系统引起的，所以与Xj成正比，设Xj=1（单位力）引起的Δij为δij，即Δij=Xjδij，上式可写成

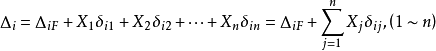
上式用矩阵形式可写为

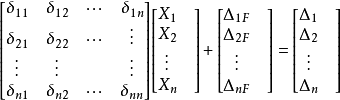
或写成更简捷的形式

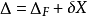式中：Δ为多余约束作用点的约束位移构成的列向量，为已知量；ΔF为外载荷（不包括多余约束力）在各约束点产生的位移列向量；X为多余约束力列向量；δ为可逆矩阵，其元素δij为Xj=1时在Xi作用点引起的位移，根据位移互等定理δij=δji ，所以δ是对称矩阵。上式称为力法正则方程，也就是用力法求解多余约束力的补充方程（组）。5