[科普中国]-迂曲度

简介

有多种多孔介质比如土壤、砂岩、生物组织、器官、纤维、海洋、地壳、颗粒床和绝缘材料等，因此在多孔介质中的流动在许多领域被关注，例如水文地质中的渗透率、土壤科学、石油开采、地球物理、聚合体的合成、化学和传热工程等。这些宏观的传输问题经常涉及到多孔介质的微观结构，迂曲度是一个微观参数，但它不仅是多孔介质微观结构的特征。弯曲管道的迂曲度通过广义的哈根方程经常涉及到渗透率。2

孔道迂曲度（tortuosity）是描述渗流通道的一个重要参数。迂曲度定义为渗流通道的实际长度与穿过渗流介质的视长度(宏观距离)的比值（如图1所示），即渗流流体质点穿越介质单位距离时，质点在孔道中运动轨迹的真实长度3。

迂曲度常被定义为

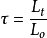
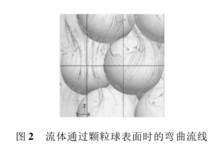式中：Lt是弯曲直线的长度；Lo是介质直线长度;然而，众所周知，通过传输介质的弯曲孔道的微观结构是非常复杂的如图2所示，图2是采用带有染色剂的流体流过多孔介质时观测到的弯曲流线图，流动路径具有随机性和不规则的特征。显然，弯曲路径微观结构是很复杂的。准确测量迂曲度非常困难。2

性质多孔介质里的物质输运特性如渗透率、电导率和热导率等通常与弯曲毛细管(流线、或电力钱、或热流线)的迂曲度(tortuosity)有关4。在工程中，可应用于计算渗流孔道的实际长度和孔道直径以及对渗透率等物性参数进行必要的修正。另外，对于多孔材料的吸声系数计算中，迂曲度也是一个重要参数。

迂曲度和渗透率的关系渗透模型是一种测量流体传导性的一种模型，传导性描述的是流体通过多孔介质的水力学行为，并且渗透率体现了迂曲度在流体阻力中的作用。迂曲度越大通过多孔介质的阻力就越大，因此渗透率就越低，从此就可以看出迂曲度和渗透率相互影响。

现在研究单相饱和流体在多孔介质中的流动。假想在满足分形分布的多孔介质内的孔隙为一束弯曲的孔道，孔道的半径满足分形分布。根据广义的Hagen － Poiseulle方程，通过单位体积内的流量是

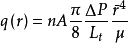
式中：q是通过单根管道的流量，n是单位面积内的管子的根数，A是截面的面积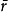，是单根管道的水利学半径的平均值，μ是流体的粘滞系数，ΔP是压强。

根据达西定律

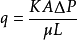
K是渗透率，孔隙率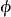是孔隙体积和多孔介质的比值

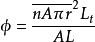
由以上公式得到

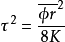
平均孔隙直径或平均毛细管半径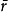也可以利用“平均水力半径”Rh来代替圆管的半径r。

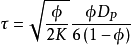
从上式看出迂曲度不仅是孔隙率的函数，还与颗粒的平均粒径以及渗透率有关，迂曲度转化为渗透率、孔隙率、粒径等的函数，这些物理量都可用实验测得，从而实现通过实验来测定迂曲度。2