[科普中国]-亥姆霍兹涡量方程

数学表示

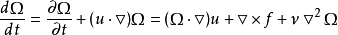
其中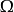，为涡量。1

物理意义方程左端为涡量的物质导数,第一项为涡量的当地变化率,第二项为涡量的迁移变化率。

等号的右侧为影响涡量变化率的各项：

第一项表示涡量与流体微团变形的相互作用。把一个长度为无穷小的涡管当作所考虑的流体微团。涡量的增强和减弱是通过涡管的伸缩和弯曲变形来实现的,因而第一项也可称为旋涡变形项。

第二项为质量力项,说明外力是影响涡量发生变化的影响因素之一。但当质量力有势时,如f=G,G为力势函数,则此项为0。由此可见有势的质量力对涡量的变化并无影响。

第三项为粘性对涡量的扩散作用，涡扩散的快慢取决于运动粘度的大小。1

方程的简化对于二维不可压流动且质量有势，该涡量方程可以简化为

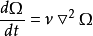若流动中粘性摩擦损失可以忽略不计，那么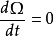，表明：在质量力有势的情况下，不可压理想流体二维流动的流场中涡量为常数，它在流动中不随时间变化。另外，引入流函数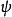，易证涡量连续方程自动满足，流函数与涡量之间的关系则满足下列关系：

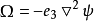将上式代入简化的涡量方程，可得

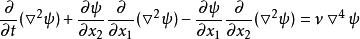该式称为涡量传递方程，涡量传递方程为四阶非线性偏微分方程，左边为惯性项，右边为粘性项。