[科普中国]-理想刚塑性材料

理想刚塑性

理想刚塑性(rigid-perfectly plastic behaviour)一种变形体模型。在弹塑性变形过程中，略去弹性变形且不考虑塑性应变增大时，应力的改变得到的应力应变关系，它是金属等材料本构关系的一种近似，按照这种本构关系，当应力未处于屈服面上时，应变为零，当应力处于屈服面上时，产生塑性流动。由于这个简化的本构关系使计算大大简化，所以它在计算结构的极限承载能力(亦称结构极限分析)和判定安定性以及金属塑性成形的力学分析中得到广泛的应用。

理想刚塑性平面应变问题1949年拜卡十夫(Batdorf)和布甸斯基(Budiansky)首先提出了滑移线理论，这是一种解析和作图相结合的方法。由于它在求解理想刚塑性平面问题的方便和有效，滑移线理论在塑性力学中占有重要的地位，一直得到较快的发展。除了对理想刚塑性平面应变问题，例如机械加工、金属冲压成型等生产上广泛应用外，近年来对平面应力问题，各向异性材料等也提出了滑移线理沦和求解方法。

应该说理想刚塑性材料是一种假设，因为真实材料在塑性加工和变形过程中存在加工硬化、蠕变和应变率以及惯性力等的影响。滑移线理论忽略这些因素，把问题作为“准静态”处理，从而导出理想化的模型，而这样的理想化理论给出了工程上很好的近似，方便求出极限荷载，与实验也比较符合，因而滑移线理沦是值得进一步深入研究和发展的塑性力学重要内容。1

理想刚塑性材料的变分原理理想刚塑性材料的变分原理也称马尔克夫（Markov）变分原理，其表述如下：对于刚塑性边值问题，在满足变形几何方程式、体积不可压缩条件式和边界位移速度条件式的所有容许速度场中，使泛函

取驻值（即一阶变分）的为本问题的精确解。

马尔克夫变分原理将上式描述的刚塑性材料的边值问题归结为能量泛函对位移速度场的极值问题，避开了偏微分方程的求解困难，一旦求得速度场的精确解后，就可以利用上式求出应变速率场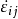，再由本构方程求出变形体瞬时的应力场。

马尔克夫变分原理是塑性力学极限分析中上限定理的另一种表达形式。它的物理意义是刚塑性变形体的总耗能率：泛函的第一项表示变形体内部的塑性变形功率，第二项表示变形体表面的外力功率。对于材料成形的塑性加工问题，外力功率主要指变形工件与模具接触界面的摩擦功率、轧制和拉拔中的张力功率等。实际上，该变分原理与力学中的最小位能原理相类似。2