[科普中国]-欧拉数

人物简介

莱昂哈德·欧拉（Leonhard Euler ，1707年4月15日～1783年9月18日），瑞士数学家、自然科学家。1707年4月15日出生于瑞士的巴塞尔，1783年9月18日于俄国圣彼得堡去世。欧拉出生于牧师家庭，自幼受父亲的影响。13岁时入读巴塞尔大学，15岁大学毕业，16岁获得硕士学位。欧拉是18世纪数学界最杰出的人物之一，他不但为数学界作出贡献，更把整个数学推至物理的领域。他是数学史上最多产的数学家，平均每年写出八百多页的论文，还写了大量的力学、分析学、几何学、变分法等的课本，《无穷小分析引论》、《微分学原理》、《积分学原理》等都成为数学界中的经典著作。欧拉对数学的研究如此之广泛，因此在许多数学的分支中也可经常见到以他的名字命名的重要常数、公式和定理。[1]此外欧拉还涉及建筑学、弹道学、航海学等领域。瑞士教育与研究国务秘书Charles Kleiber曾表示：“没有欧拉的众多科学发现，今天的我们将过着完全不一样的生活。”法国数学家拉普拉斯则认为：读读欧拉，他是所有人的老师。[2]2007年，为庆祝欧拉诞辰300周年，瑞士政府、中国科学院及中国教育部于2007年4月23日下午在北京的中国科学院文献情报中心共同举办纪念活动，回顾欧拉的生平、工作以及对现代生活的影响。2

拓扑学中的欧拉数

最通常的空间完整性，即空洞区域内空洞数量的度量，测量法称为欧拉函数，它只用一个单一的数描述这些函数，称为欧拉数。数量上，欧拉数=（空洞数）-（碎片数-1），这里空洞数是外部多边形自身包含的多边形空洞数量，碎片数是碎片区域内多边形的数量。有时欧拉数是不确定的。

线性代数中的欧拉数线性代数中，欧拉数是对向量丛的一种刻画。有向向量丛的零截面对于底空间的相交数。设ξ=(E，π，M)是n维有向向量丛，M是n维紧致连通有向(无边)微分流形。若将底空间M与ξ的零截面的像等同，则：

χ(ξ)=#(M，M)=#(M，M;E)

称为向量丛ξ的欧拉数。设M如上述，ξ=TM，则χ(ξ)称为流形M的欧拉特征，记为χ(M)。例如，χ(S……2n)=2(因而S^2n上任何向量场均有零点)，χ(S)=0.欧拉数是向量丛的同构不变量.在流形的切丛情形，得到在代数拓扑中有广泛应用的拓扑不变量——流形的欧拉特征数。

数学中的欧拉数数学中，欧拉数是一组重要的常数，即函数sech t在t=0点的泰勒展开式：

的系数En。前几个欧拉数为：

E0=1，E1=1，E2=5，E3=61，E4=1385，E5=50521，E6=2702765，……

欧拉数与欧拉多项式En(x)有关，

有时也称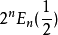 为欧拉数。3

流体力学中的欧拉数流体力学中欧拉数的符号为Eu，描述动量传递的特征数。

Eu=gcΔP/ρu2(若采用英制单位，gc为转换比率，单位为lb.ft/lb.hr2),

Eu=ΔP/ρu2(若采用标准单位，不需加转换比率)

其中Eu定义为欧拉数。△p为压力差;ρ为物体的体积质量;υ为特征速度。SI单位：1(一)。与通常量的符号的表达不同的是，特征数的符号均由两个字母组成。当特征数符号在乘积中作为相乘的因数时，建议其符号与其他符号之间空一个间隔，或用乘号或括号隔开。

它反映了流场压力降与其动压头之间的相对关系，体现了在流动过程中动量损失率的相对大小。4