[科普中国]-分波前法

定义

波前是指波的等相位面达到的空间。分波前干涉法就是选择空间不同两点的光波作为干涉源，实现干涉。根据惠更斯原理，空间任何一个闭合面都可以作为次级波源，远处的光波是次级波源发出的光波的干涉叠加。分波前正是相当于在这样的闭合曲面上取至少两个不同区域让光透过，以实现干涉。1

典型例子最典型的分波前干涉法，有杨氏双缝隙干涉、双孔干涉、光栅干涉。1

限制和应用分波前法是否出现干涉条纹，受光源的空间相干性限制。点光源具有最好的空间相干性，在全空间相干，因此，分波前时可以取距离任意远的区域的波前都能得到干涉条纹。扩展光源空间相干性不高，分波前时，取的不同区域只有局限在空间相干性良好的范围内才能得到干涉条纹。根据这一定，分波前法又可以测量光场的空间相干性，从而推测出光源的大小。用空间相干性判断光源大小的最好例子是迈克尔逊星体干涉仪。1

分波前法干涉杨氏干涉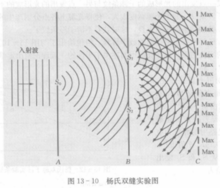1801年，英国人托马斯·杨用一个普通光源实现了光的干涉，由于其构思之巧妙，装置之简单，条纹之明显，使得这个实验在波动光学中具有十分重要的意义，它成为光的波动学说的立论基础之一，被誉为物理学中最美的实验之一。

杨认为，虽然每个发光的分子或原子发出的光时断时续，各个光波的初相位各不相同，但是从同一个光波分开的两束光应有恒定的相位关系，这就是分波前法干涉。因此，他使一个点光源发出的光通过两个小孔，将其分成两个部分，让它们重新相遇而叠加，结果在屏上观察到了干涉条纹。杨氏干涉的实验简图如图1所示。

在图1中，平面单色入射光通过小孔S0，造成一个点光源，由光源S0发出的光波的波前同时到达小孔S1和S2，通过S1和S2后的两束光在屏C上相遇时出现了如图2（a）所示的干涉现象。由于S1和S2位于S0发出的光波的同一个波前，S1和S2就可以视为两个新的相干的子光源，它们发出的两束光满足相干条件，因而出现了干涉现象。这种从同一个波前上获得相干光的方法称为分波前法。

后来，杨氏用三条狭缝代替上述的三个小孔，每个狭缝相当于一个线光源，其可以认为是由多个点光源沿一条线排列而成。由于每个点光源经双缝后均产生干涉图样，而这些点光源与双缝的相对位置完全相同，它们产生的干涉图样也完全相同。这些相同的图样相互叠加起来就使亮点变成亮线，如图2（b）所示，从而使干涉详细更为清晰。2

洛埃镜实验受杨氏实验的启发，人们又先后提出了菲涅耳双棱镜实验、菲涅耳双平面镜实验和洛埃镜实验等多种实验方案，这些实验都属于分波前法干涉，它们无一例外地显示出了光的干涉现象。其中洛埃镜实验最值得引起注意，因为它还显示了光波动性的另一种现象——半波损失现象。

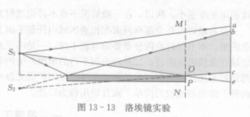洛埃(H．Lloyd，1800-1881)在1834年提出的实验方案更加简单，他用一块平板玻璃作反射镜，用一个狭缝状光源作为干涉用光源。从狭缝光源发出的光波一部分掠射(即入射角接近90°)到平板玻璃上，经表面反射到达屏上，另一部分直接射到屏上，这两部分光在屏上相遇叠加，出现了干涉条纹，如图3所示。

在这个实验中，反射光可看做是由虚光源S2发出的，S1与S2这一对镜像光源构成了一对相干光源。有趣的是，若把屏幕移到镜面边缘处(即MN的位置)，在屏幕与反射镜的交点O处出现了暗条纹。这一点令人始料不及，因为按照前述干涉的一般理论，由S1与S2发出的两个光波到达O点相遇时光程差为零，O点应出现明条纹。出现暗条纹的实验事实说明了由S1发出的光经镜面反射时一定多走或少走了λ0/2的光程，使得直射光和反射光在O点叠加时满足暗条纹的条件。这种光在镜面反射时相位发生突变的现象称半波损失现象(half-wave loss)。

光的半波损失现象得到了其他实验的进一步证明。现在已经确认，当光在光疏媒质和光密媒质界面反射时，反射光的光程要产生λ0/2的突变。光的半波损失现象可以由光的电磁理论给出合理的解释，因而它成为光的波动说的又一个实验证据。2