[科普中国]-谐波平衡法

简述

原始的谐波平衡法，其基本原理是将动态方程的每一状态变量用一个傅氏级数来表示，以满足其周期性的要求。然后，应用优化算法、优化傅氏级数的系数，使得系统方程具有最小的误差。2

算法在各种近似解析方法中，谐波平衡法是概念最明了，使用最简便的近似方法，而且应用范围不仅限于弱非线性系统，也适用于强非线性系统。该方法的基本思想是认为在非线性系统中尽管存在非线性因素的影响，但在一定条件下其定常解仍然是近似简谐的。

设有非线性方程

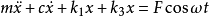式1

若式1存在着周期为r或者丁的整数倍的周期解的情形，方程右边Fcosωt在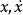的有限区域内分别满足莱布尼茨条件，则方程的解是唯一的，且分段可微的，因此方程的解可展成傅立叶(J．B．J．Fourier)级数，故设为

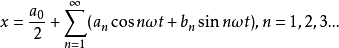式2

将式2代入方程1的两边，方程两边同阶谐波项的系数相等，从而得到包含未知数的一系列代数方程，如果只取N次谐波，则可得2N+1个方程，由此可求出含有N次谐波的近似解。

谐波平衡法解的精度取决于谐波项个数的选取。当谐波项项数选取得过多时，则要求求解一个多自由度高阶的非线性方程组，导致求解困难；当谐波项数取得太少(如只取一个谐波项)时，则会引起比较大的误差。针对谐波平衡法这个缺点，Lau和Cheung于1981年提出了增量谐波平衡法(IHB法)，广泛应用于求解各种非线性振动问题。3

应用随着无线通信的发展，射频电路逐渐得到了广泛应用。在射频电路设计中，通常需要得到射频电路在信号激励下的稳态响应。如果采用传统的SPICE模拟器对射频电路进行模拟，为了得到电路的稳态响应，通常需要经过很长的瞬态模拟时间，电路的响应才会稳定。 对于射频电路的稳态响应，可以采用特殊的模拟技术在较短的时间内获得，谐波平衡法就是其中之一。
我们知道，在频域中要描述象三极管、二极管那样的非线性器件是非常困难的，然而，我们能容易的在时域中得到非线性元件的非线性模型。因此，在谐波平衡仿真器中，非线性系统在时域中描述，而线性系统在频域中描述，FFT则是联系时域和频域的一座桥。
谐波平衡分析法是一种混合的频域∕时域分析技术，将时域和频域通过 FFT 结合起来，它将电路状态变量近似写成傅立叶级数展开的形式，通常展开项必须取得足够大，以保证高次谐波对于模拟结果的影响可以忽略不计。谐波平衡法在目前的商用RF软件中得到了很好的应用，如ADS、AWR、HSpice、Nexxim等都支持HB分析。
谐波平衡仿真是非线性系统分析最常用的分析方法，用于仿真非线性电路中的噪声、增益压缩、谐波失真、振荡器寄生、相噪和互调产物，它要比SPICE基仿真器快得多，可以用来对混频器、振荡器、放大器等进行仿真分析。

对放大器而言，采用谐波平衡法分析的目的就是进行大信号的非线性模拟。通过它可以模拟电路的1dB输出功率、效率以 及IP3等与非线性有关的量。