定义
在机械振动中,回复力为0的位置叫做这个简谐运动的平衡位置(position of equilibrium),该位置处速度最大,动能最大,势能为0。
力学系统平衡位置在平衡状态的力学系统受到微扰后由于其平衡位置的特殊性而引起的稳定性问题。若不论时间多长,受微扰后的系统对原位置的偏差能随初始扰动的减小而受到任意指定的限制,则此位置是稳定的;反之,该位置是不稳的。例如小球在竖立的圆形轮圈上有两个平衡位置,致高点A是不稳定位置,最低点B是稳定位置。
1644年E.托里拆利发现,当物体系统的重心处于最低位置时,该系统是平衡的。托里拆利的“平衡”只指稳定的平衡。平衡位置的稳定性可看成运动稳定性的特例。
一个力学系统可有几个平衡位置,有些是稳定的,有些是不稳定的。一个有n个自由度的完整系统,其位置由n个广义坐标 ,
, ,…,
,…, 来确定。要研究系统的稳定性,一般可通过坐标变换,使所要讨论的一个平衡点正好是坐标系的原点,对这原点有:
来确定。要研究系统的稳定性,一般可通过坐标变换,使所要讨论的一个平衡点正好是坐标系的原点,对这原点有: =
= =…=
=…= =0和妜1=妜2= … =妜n=0。又由于力系平衡,因此各广义力
=0和妜1=妜2= … =妜n=0。又由于力系平衡,因此各广义力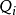 为零,即
为零,即
 =
=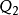 = …=
= …= =0。
=0。
对原点为平衡点的情况,坐标 ,
, ,…,
,…, 就表示离开这位置的偏差。系统平衡稳定性的定义是:设在时间t=t0有一扰动,使系统产生偏差
就表示离开这位置的偏差。系统平衡稳定性的定义是:设在时间t=t0有一扰动,使系统产生偏差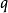 和妜(i=1,2,…,n)。如果对于任意ε>0可找出
和妜(i=1,2,…,n)。如果对于任意ε>0可找出 =
= (t)>0,使
(t)>0,使
|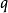 |
|




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国