简介
单位体积的弹性应变能称为弹性应变能密度。1
弹性应变能和应变能密度弹性体受外力作用后,不可避免地要产生变形,同时外力的势能也要产生变化。根据热力学的观点,外力所做的功,一部分将转化为弹性体的动能,一部分将转化为内能;同时,在物体变形过程中,它的温度也将发生变化,或者从外界吸收热量,或者向外界发散热量。现分析弹性体内任一有限部分∑的外力功和内能的变化关系,设弹性体内取出部分Σ的闭合表面为S,它所包围的体积为V。以δW表示外力由于微小位移增量在取出部分Σ上所作的功,δU表示在该微小变形过程中取出部分Σ的内能增量,δK表示动能增量,δQ表示热量的变化(表示为功的单位),根据热力学第一定律,则有
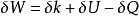
我们首先假设弹性体的变形过程是绝热的,也就是假设在变形过程中系统没有热量的得失。再假设弹性体在外力作用下的变形过程是一个缓慢的过程,在这个过程中,荷载施加得足够慢,弹性体随时处于平衡状态,而且动能变化可以忽略不计(这样的加载过程称为准静态加载过程),则根据上式表示的热力学第一定律,外力在变形过程中所做的功将全部转化为内能储存在弹性体内部。这种贮存在弹性体内部的能量是因变形而获得的,故称之为弹性变形能或弹性应变能。由于弹性变形是一个没有能量耗散的可逆过程,所以,卸载后,弹性应变能将全部释放出来。下面,推导单位体积弹性应变能的表达式。
仍以X、Y、Z表示单位体积的外力,表示作用在弹性体内取出部分Σ表面上单位面积的内力。对上述的准静态加载过程,可以认为弹性体在外力作用下始终处于平衡状态。外力所作的功W包含两个部分:一部分是体力X、Y、Z所作的功W1,另一部分是面力所作的功W2,它们分别为
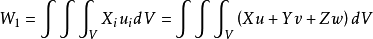
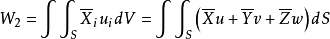
故
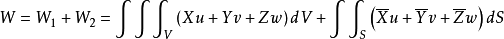
因此,外力由于微小位移增量在取出部分Σ上所作的功δW 可以表示为
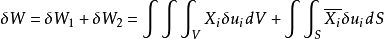
将平衡微分方程和静力边界条件代入上式,并利用散度定理,上式可化为
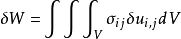
最终可推得相应的内能增量δU为
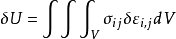
定义函数u0(εij),使之满足
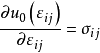
该定义式称为格林(Green)公式。
则有 。
。
由上式可以看出,函数u0(εij)表示单位体积的弹性应变能,故称之为弹性应变能密度函数(或弹性应变比能函数),简称为应变能。由于弹性应变能密度函数表示弹性体的内能概念,因此,它必然是一个势函数,故也称之为弹性势函数。
对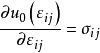 取积分可得
取积分可得
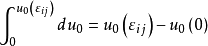
这里,u0(εij)和u0(0)分别表示物体变形之后和未变形时的弹性应变能密度。通常,取u0(0)=0,于是有
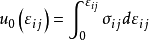
根据格林公式,假如u0(εij)的具体函数形式能够确定的话,那么,弹性体的应力与应变之间的关系也就完全确定了。这表明,弹性应变能密度函数是弹性材料本构关系的另一种表达形式。2
轴向拉压杆的应变能和应变能密度
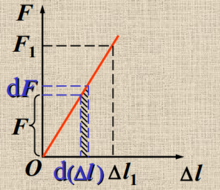
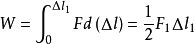
应变能: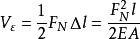 。
。
应变能密度:杆件应变能与杆件体积之比。
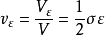
应变能 —— 是杆件参数,与杆件变形有关。
应变能密度 —— 与杆件无关,只与应力状态有关。3
三向应力状态的应变能密度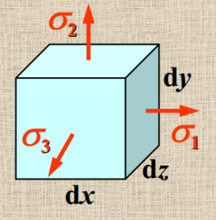
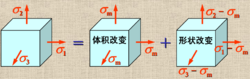
应变能密度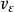 =体积改变能密度
=体积改变能密度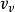 +形状改变能密度
+形状改变能密度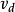 。
。
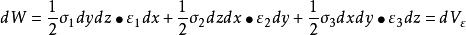
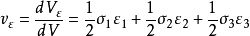
体积改变能密度:
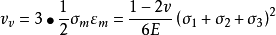
形状改变能密度:
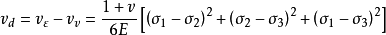




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国