概念
切线刚度阵是广义力对广义位移的一阶导数,即应力应变曲线的切线,对于非线性材料无法得到准确的刚度矩阵,可以用切线刚度矩阵代替。
非线性稳定性分析中常用到割线刚度矩阵与切线刚度矩阵,其中,前者用于全量形式的平衡方程,后者用于增量形式的平衡方程。切线刚度矩阵常用于判断临界点的稳定性和对临界点进行分类。基于有限元法,考虑了结构可能存在初始缺陷的情况,从结构的能量表达式出发,推导了二者之间的数学关系。具体做法是:针对具有任意多自由度和任意参数变量(如任意荷载或初始缺陷)的结构,从结构的通用总势能泰勒级数展开式出发,推导得出结构的切线刚度矩阵和割线刚度矩阵之间的数量关系。
基本原理注意到 ,由
,由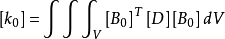 式子积分得到
式子积分得到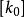 ,而由
,而由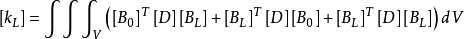 式子可求得
式子可求得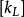 ,又由
,又由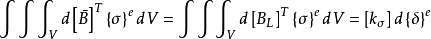 式子,则有:
式子,则有:
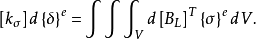
由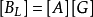 式子,可得:
式子,可得:
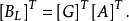
注意到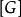 不含
不含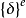 ,由上式得:
,由上式得:
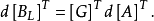
将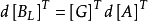 代入
代入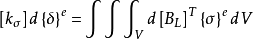 式子的右端,则:
式子的右端,则:
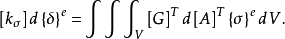
利用 和
和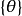 的第二个性质,得:
的第二个性质,得:
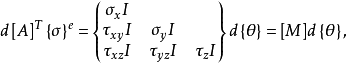 式中
式中
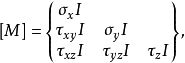 而
而 为三阶单位矩阵。
为三阶单位矩阵。
由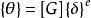 式子可得:
式子可得:
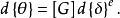
将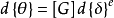 代入
代入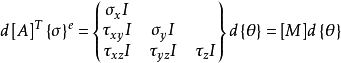 式子中,可得:
式子中,可得:
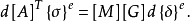
再将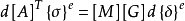 代入
代入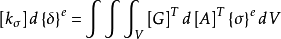 式子中,便得到具有对称形式的初应力矩阵
式子中,便得到具有对称形式的初应力矩阵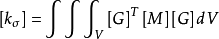 。
。
至此,三维单元的切线刚度矩阵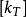 就可由下式求得:
就可由下式求得:




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国