[科普中国]-双曲余弦函数

定义

从原点发出的射线与单位双曲线（方程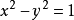：）相交于点（cosh a,sinh a)。这里的a为射线、双曲线和x轴围成的面积的两倍。对于双曲线上位于x轴下方的点，这个面积被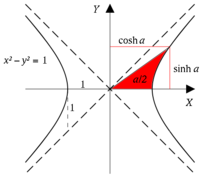认为是负值。其中，cosh a就是a的双曲余弦函数。

经过复杂的计算可以推出： 。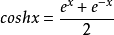

性质定义域与值域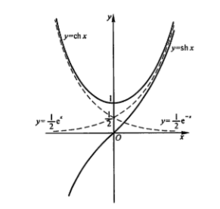

双曲余弦函数的定义域为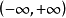 。1值域为[1, 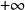)。当x=0时，取到最小值1。

奇偶性双曲余弦函数在定义域内是偶函数。1可以证明。

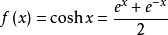
取x的负值。又得：

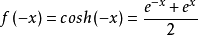
根据加法交换律，可得出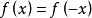 。根据偶函数的定义，可知该函数是偶函数。它关于y轴对称。

单调性双曲余弦函数y=cosh x，在区间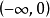 内它是单调减少的，在区间 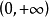内它是单调增加的。cosh 0=1是该函数的最小值。1

可以用导数证明。

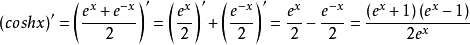
由于分母是永远大于0的，而分子中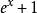 也是永远大于0。只有 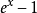在x=0时是等于0。在x0。得出当x0时，双曲余弦函数的导数永远大于0。那么它在 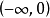内单调递减的，在 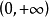内单调递增。在x=0时，最小值为1。无最大值。

周期性无论是双曲余弦函数y=cosh x，还是双曲正弦函数y=sinh x、双曲正切函数y=tanh x，它们都不是周期函数。

凹凸性由于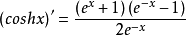

那么双曲余弦函数的二阶导数为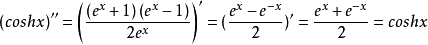

可见双曲余弦函数的二阶导数是它本身。而双曲余弦函数的值域是[1,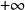 )。那么双曲余弦函数的二阶导数在实数集R上恒大于0。

而根据函数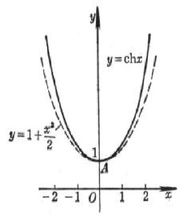凹凸性的判定方法（定理）：

设f(x)在[a,b]上连续，在（a,b）内具有一阶导数和二阶导数，那么：

（1）若在（a,b）内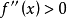， ，则f(x)在[a,b]上的图形是凹的。

（2）若在（a,b）内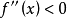， ，则f(x)在[a,b]上的图形是凸的。2

根据上面的函数凹凸性判断定理。得出那么无论是在那个单调区间，双曲余弦函数都是凹函数

高数中应用导数双曲余弦函数的导数是双曲正弦函数。即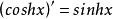

也可以转化为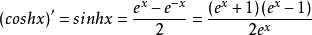

不定积分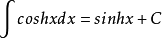 3 其中，C为常数。可见，双曲余弦函数的不定积分，除去常数C，也是双曲正弦函数。

另有公式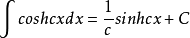 (这里，大写的C为常数）

另外，关于双曲余弦函数还有如下的公式：
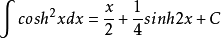(其中，C为任意常数）4

泰勒展开式双曲余弦函数的泰勒展开式为：

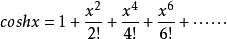即：

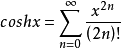
反函数双曲余弦函数的反函数是反双曲余弦函数。它记作arcoshx。根据反函数的定义，它的定义原本应该是：

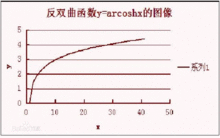其中，x满足条件： 。

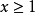反双曲余弦函数的图像原本有x轴上方的一支和x轴下方的一支。即且这两支关于x轴对称。但是，这样子会造成一个自变量x对应两个函数值，不符合函数的定义。

为了符合函数的定义，一般取x轴上方的那一支。因而得到了反双曲余弦函数的定义式。

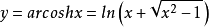
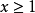
双曲余弦的反函数，即反双曲余弦函数y=arcoshx的定义域为[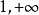 ),它在区间[ 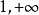)上是单调增加的。5

图像如上图。它是一条有点像抛物线（二次）但不是抛物线的曲线。因这条曲线与两端固定的绳子（或铁链）在均匀引力作用下下垂相似。这条曲线称作悬链线。悬链线就是双曲余弦函数的图像。

悬链线的数学表达式为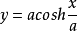 。其中，a为常数。当a=1时，所得的函数（图像）正好是双曲余弦函数（图像）。

公式两角和和两角差的公式sinh(x+y)=sinhxcoshy+coshxsinhy

sinh(x-y)=sinhxcoshy-coshxsinhy

cosh(x+y)=coshxcoshy+sinhxsinhy

cosh(x-y)=coshxcoshy-sinhxsinhy1

二倍角公式双曲余弦和双曲正弦的二倍角公式。

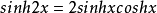
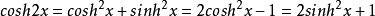
三倍角公式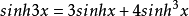

推导：

1、双曲正弦的三倍角公式：

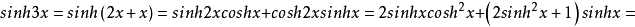
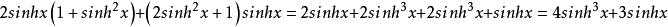
2、双曲余弦的三倍角公式：

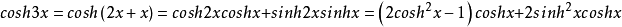
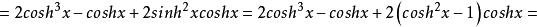
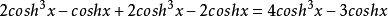
半角公式双曲余弦以及双曲正弦的半角公式有：

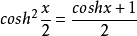
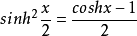
恒等式等式1：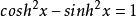

等式1的证明：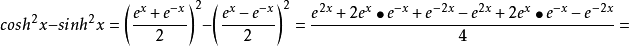

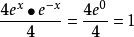
等式2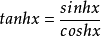： （双曲正切的定义式，与三角函数中的正切类似）

等式3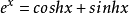： （双曲函数和指数函数的关系）

等式4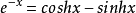： （双曲函数和指数函数的关系）