[科普中国]-若尔当曲线

简介

简单曲线通俗说来即指的是：这条曲线不和自身相交。2

若当定理：平面上一条闭合（首尾相接）的若尔当曲线，把平面分成2个区域，并且如果在这两个区域内分别取一点，再用一条曲线将其相连，则这条连线必定和原来的闭合若尔当曲线相交。它的证明需要用到拓扑学的知识。

若尔当曲线是以数学Jordan的名字命名，它又翻译为：若当曲线，乔丹曲线，约当曲线等3

若尔当定理平面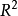中的若尔当曲线或简单闭合曲线是圆在平面中的映射C，即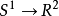：。 平面上一条闭合（首尾相接）的若尔当曲线，把平面分成2个区域，并且如果在这两个区域内分别取一点，再用一条曲线将其相连，则这条连线必定和原来的闭合若尔当曲线相交。

或者，若尔当曲线是φ：[0,1]→R2上的连续映射，使得φ（0）=φ（1），并且φ至[0,1]的限制是认可的。 前两个条件说C是连续循环，而最后一个条件规定C没有自交点。

通过这些定义，约旦曲线定理可以表示如下：

令C为平面R2中的若尔当曲线。 那么它的整个区域由两个相连的部分组成。 这些部分中的一个是有界的（内部），另一个是无界的（外部），曲线C是每个部分的边界。4

证明和推论若尔当曲线定理被H. Lebesgue和L.E.J.独立地推广到更高的维数。 Brouwer在1911年，推导出了Jordan-Brouwer分离定理：

令X是（n + 1）维欧几里得空间Rn + 1（n> 0）中的拓扑球，即n球Sn注入到Rn + 1中的注入连续映射的图像。那么Rn + 1中X的互补部分Y由两个连接的部分组成。这些部分中的一个是有界的（内部的），另一个是无界的（外部的）。集合X是它们的共同边界。

证明使用同源性理论。首先确定，更一般地说，如果X与k同位，则Y = Rn + 1 \ X的缩小的积分同源性组如下：5

这通过使用Mayer-Vietoris序列在k中的归纳证明。当n = k时，Y的同质性减少为1，这意味着Y具有2个连通分量（此外，路径连接），并且有一点额外的工作，一个表明它们的共同边界是X. JW亚历山大发现了进一步的泛化，他建立了Rn + 1的紧凑子集X的减少的同源性和其补体减少的同源性之间的亚历山大二重性。如果X是没有边界的Rn + 1（或Sn + 1）的n维小型连接子集，则其补码具有2个连接分量。

若尔当曲线定理有一个加强，称为若尔当 - 施诺因定理，其中指出，由R2中的约旦曲线确定的内部和外部平面区域与单位盘的内部和外部是同构的。特别地，对于内部区域中的任何点P和约旦曲线上的点A，存在将P与A连接的Jordan弧，并且除了端点A之外，完全位于内部区域中。 Jordan-Schönfly定理的一个替代和等价的公式表明，任何若尔当曲线φ：S1→R2，其中S1被看作平面中的单位圆，可以扩展到平面的同构ψ：R2→R2。不像Lebesgues和Brouwer对若尔当曲线定理的泛化，这个说法在更高的维度上变得虚假：虽然R3中的单位球的外部是简单的连接，因为它缩回到单位球体上，亚历山大角球是R3的一个子集与球体同胚，但是在空间上如此扭曲，其R3中的补体的无界分量不是简单地连接，因此不能与单体球的外部同胚。6

历史和进一步证明首先，若尔当曲线定理的陈述似乎是显而易见的，但它是一个相当困难的定理来证明。伯纳德·博尔扎诺（Bernard Bolzano）是第一个拟定一个精确猜想的人，认为这不是一个不言而喻的陈述，但它需要一个证明。对于多边形线，很容易建立这个结果，但问题出现在各种不良行为曲线中，其中包括无差异曲线，如科赫雪花和其他分形曲线，甚至是由奥斯古德（1903）建造的正面积的若尔当曲线。

这个定理的第一个证明是卡米尔·乔丹在他的真实分析讲座中给出的，并在他的书“分析科学技术学院”中发表。若尔当的证据是否完整，有一些争议：大多数评论家都声称，奥斯瓦尔德·凡勃伦（Oswald Veblen）后来提出了第一个完整的证明。

然而，他的证明对许多数学家来说是不能令人满意的。它在一个简单的多边形的重要特殊情况下就没有证明这个定理，而从这一点来看，至少必须承认所有细节都没有给出。

不过，Thomas C. Hales写道：

几乎每一次我发现的现代引文都同意，第一个正确的证明是由于Veblen ...鉴于对若尔当证据的沉重批评，当我坐下来阅读他的证据，没有发现任何令人反感的时候，我感到惊讶。从那时起，我已经联系了一些批评若尔当的作者，每一案件都是作者承认没有直接了解若尔当证据的错误。

哈尔斯还指出，简单多边形的特殊情况不仅是一个容易的运动，而且还没有真正用于若尔当，引用迈克尔·雷肯说：

若尔当的证明基本上是正确的...若尔当的证明不能以令人满意的方式呈现细节。但是这个想法是正确的，有了一些抛光，证明将是无可挑剔的。

若尔当的证据和de laVallée-Poussin的另一个早期证明后来被Schoenflies（1924）批评性地分析和完成。

由于若尔当曲线定理在低维拓扑和复杂分析中的重要性，受到20世纪上半叶突出数学家的关注。定理及其概括的各种证明由J.W Alexander，Louis Antoine，Bieberbach，Luitzen Brouwer，Denjoy，Hartogs，BélaKerékjártó，Alfred Pringsheim和Arthur Moritz Schoenflies构建。

若尔当曲线定理的新的基本证明以及早期证明的简化仍在继续进行。

Filippov（1950）和Tverberg（1980）提出了基本证据。

使用Narens（1971）的非标准分析的证明。

Gordon O. Berg，W. Julian和R. Mines等人使用建构性数学的证据。 （1975年）。

使用昭和（1984）Brouwer定点定理的证明。

Thomassen（1992）给出了使用完整二分图K3,3的非平面性的证明。

若尔当曲线定理的第一个正式证明是由Hales（2007a）于2005年1月在HOL Light系统中创建的，并包含约6万行。 2005年由国际数学家团队使用Mizar系统制作了另外严格的6,500线的正式证明。 Mizar和HOL Lightproof都依赖于以前证明的定理的库，所以这两种尺寸都不可比。坂本松本和横田洋田（2007）显示，若尔当曲线定理在证明理论强度方面与弱科德格引理相当。7