[科普中国]-反正弦函数

简介

在数学中，反三角函数（偶尔也称为弓形函数（arcus functions），反向函数（antitrigonometric functions）或环形函数（cyclometric functions）是三角函数的反函数（具有适当的限制域）。 具体来说，它们是正弦，余弦，正切，余切，正割和辅助函数的反函数，并且用于从任何一个角度的三角比获得一个角度。 反三角函数广泛应用于工程，导航，物理和几何。

反正弦函数（反三角函数之一）为正弦函数y=sinx（x∈[-½π,½π]）的反函数，记作y=arcsinx或siny=x（x∈[-1,1]）。由原函数的图像和它的反函数的图像关于一三象限角平分线对称可知正弦函数的图像和反正弦函数的图像也关于一三象限角平分线对称。12

公式用x表示自变量，用y表示因变量（函数值）时，正弦函数

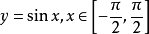
的反函数叫做反正弦函数，记作

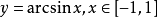
图像由原函数的图像和它的反函数的图像关于一三象限角平分线对称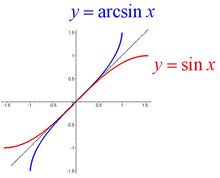，知正弦函数的图像和反正弦函数的图像也关于一三象限角平分线对称。

作图：先画出函数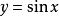 在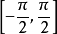 上的图像，用平板玻璃或透明纸描好图像，翻转过来。（如图所示）

性质定义域反正弦函数的定义域为

值域反正弦函数的值域

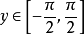
单调性反正弦函数是单调递增函数。

证明。法一：

因为

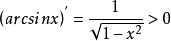
证毕。

**法二：**令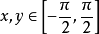 且 ，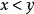

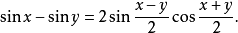
因为

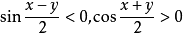
即

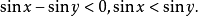
于是正弦函数在该区间上为增函数。所以，由反函数的性质，反正弦函数为增函数。

证毕。

奇偶性反正弦函数是奇函数。即

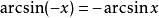
证明。知在反正弦函数的值域上，正弦函数是奇函数，则反正弦函数也是奇函数。证毕。

导函数反正弦函数的导函数

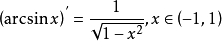
且

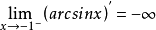
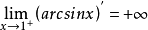
运算性质反三角函数的三角函数如下式所示。 推导它们的一个快速方法是通过考虑直角三角形的几何形状，其长度为1的一侧，长度x的另一侧（0和1之间的任何实数），然后应用毕达哥拉斯定理和三角比。

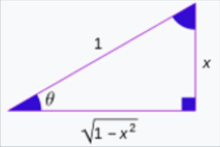
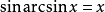
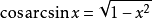
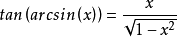
反三角函数之间的关系互补角度：

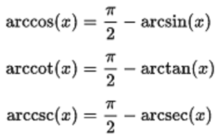
负参数：

倒数参数：

在微积分反三角函数的导数z的复数值的导数如下3：

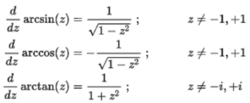
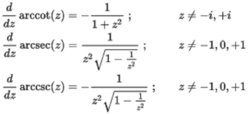
无穷级数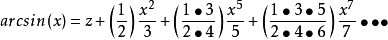

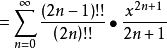
应用找到一个直角三角形的角度当三角形边的长度已知时，当尝试确定直角三角形的剩余两个角度时，反三角函数是有用的。 回想起正三角形的正确定义，例如，

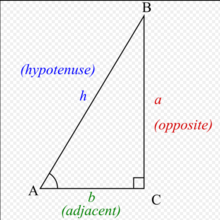
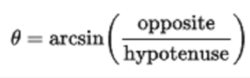
通常，斜边是未知的，需要使用毕达哥拉斯定理在使用反正弦或反曲线之前进行计算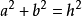： 其中h是斜边的长度。 在这种情况下，反正切是有用的，因为斜边的长度是不需要的。

例如，假设当屋顶耗尽20英尺时，屋顶会下降8英尺。 屋顶与水平面形成一个角度θ，其中θ可以如下计算：

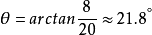
数值精度对于0和π附近的角度，秋水仙素受到病态调节，从而计算出计算机实现中精度降低的角度（由于位数有限）. 类似地，对于π/ 2和π/ 2附近的角度，反正弦不准确。4