[科普中国]-等腰直角三角形

概念

等腰直角三角形是特殊的等腰三角形，它的特点是：

（1）两底角等于45°。

（2）两腰相等。

（3）等腰直角三角形三边比例为。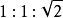

性质等腰直角三角形是特殊的等腰三角形（有一个角是直角），也是特殊的直角三角形（两条直角边等），因此等腰直角三角形具有等腰三角形和直角三角形的所有性质（如三线合一、勾股定理、直角三角形斜边中线定理等）。

当然，等腰直角三角形同样具有一般三角形的性质，如正弦定理、1余弦定理、角平分线定理、中线定理等。等腰直角三角形三边比例为。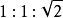

等腰直角三角形的判定方法一：

根据定义，有一个角是直角的等腰三角形，或两条边相等的直角三角形是等腰直角三角形。

方法二：

三边比例为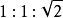的三角形是等腰直角三角形。

证明：2勾股定理的逆定理可知该三角形是直角三角形，并且有两条边相等，满足等腰直角三角形的定义。

方法三：

底角为45°的等腰三角形是等腰直角三角形。

证明：用三角形内角和定理求出角度分别为45°、45°、90°，满足等腰直角三角形的定义。

方法四：

有一个锐角是45°的直角三角形是等腰直角三角形。

证明同方法三。

方法五：

直角边和斜边的比例为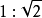的直角三角形是等腰直角三角形。

证明：根据勾股定理求出另一条直角边也是1，利用方法二判定。或根据反三角函数求出直角边所对角为45°，利用方法四判定。

方法六：

有一个角是45°，并且这个角两边长度比为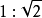的三角形是等腰直角三角形。

证明：根据馀弦定理可求出第三边长为1，利用方法二判定。

方法七：

有一个角是45°，并且这个角所对的边和它的一条边长度比为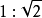的三角形是等腰直角三角形。

证明：和方法六不同，如果长度为1的边不是45°角的邻边而是对边，则根据正弦定理求出长度为√2的边所对角为90°，再利用方法四判定。

特殊等腰直角三角形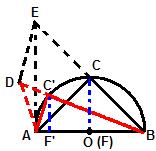

斜边相等的直角三角形中，以等腰直角三角形的面积和周长最大。

解:首先证明面积最大的是它

将等腰Rt△ACB,任意Rt△AC'B都画出外接圆,AB为圆的直径。(其实这样做是为了满足斜边AB相等,且是直角三角形).再做CF⊥AB,C'F⊥AB.(蓝色辅助线)

由三线合一可知O和F重合，且易证OC>C'F'(根据垂径定理和直径是最长的弦得到)。

而CF是△ABC的高,C'F'是△ABC'的高,由面积公式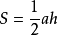可知等腰Rt△ABC面积最大。

其次解:证明周长最大的还是它

延长BC到E,使CE=CA.延长BC'到D,使C'D=C'A.连接DE,AD,AE.

∵AC'⊥BD,AC⊥BE

∴△AC'D,△ACE都是等腰直角三角形

∴∠AEB=∠ADB=45°

∵D,E在线段AB同侧

∴ABED四点共圆

∵AC=BC=CE

∴∠EAB=90°(直角三角形斜边中线定理逆定理)

∴∠EDB=90°

∴BE>BD

又∵EB=AC+CB. BD=AC'+C'B.

∴AC+CB>AC'+C'B.

∵Rt△ACB周长=AB+(AC+CB).

Rt△AC'B周长=AB+(AC'+C'B).

∴等腰Rt△ABC周长最大。