[科普中国]-狄利克雷分布

简介

狄利克雷（1805～1859） Dirichlet，Peter Gustav Lejeune 德国数学家。对数论、数学分析和数学物理有突出贡献，是解析数论的创始人之一。1805年2月13日生于迪伦，1859年5月5日卒于格丁根。中学时曾受教于物理学家G.S.欧姆；1822～1826年在巴黎求学，深受J.-B.-J.傅里叶的影响 。回国后先后在布雷斯劳大学、柏林军事学院和柏林大学任教27年，对德国数学发展产生巨大影响。1839年任柏林大学教授，1855年接任C.F.高斯在哥廷根大学的教授职位。

在分析学方面，他是最早倡导严格化方法的数学家之一。1837年他提出函数是x与y之间的一种对应关系的现代观点。

在数论方面，他是高斯思想的传播者和拓广者。1836年狄利克雷撰写了《数论讲义》，对高斯划时代的著作《算术研究》作了明晰的解释并有创见，使高斯的思想得以广泛传播。1837年，他构造了狄利克雷级数。1838～1839年，他得到确定二次型 类数的公式。1846年，使用抽屉原理。阐明代数数域中单位数的阿贝尔群的结构。

在数学物理方面，他对椭球体产生的引力、球在不可压缩流体中的运动、由太阳系稳定性导出的一般稳定性等课题都有重要论著。1850年发表了有关位势理论的文章，论及著名的第一边界值问题，现称狄利克雷问题。

狄利克雷分布奠定了狄利克雷过程的基础，被广泛应用于自然语言处理特别是主题模型（topic model）的研究。2

数学定义K阶狄利克雷分布的概率密度函数表示为如下形式：

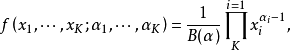其中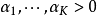， 为参数。概率密度函数定义在（K-1）维单纯形上：

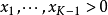
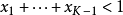
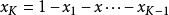归一化常数为对变量Beta函数，可以用Gamma函数来表示：3

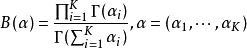
性质狄利克雷分布有个重要的性质就是聚合性（agglomerative property）4，即假设如下狄利克雷分布：

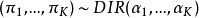
那么，如果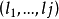 是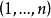 的任意一个划分，那么有：

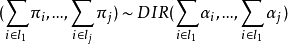
这个性质使得该分布在计算中非常方便，因而运用广泛。5

直观的参数表述浓度参数Dirichlet分布经常用作贝叶斯推理中的先前分布。最简单或最常见的Dirichlet类型是对称的Dirichlet分布，其中所有参数相等。这对应于您没有任何先前信息有利于一个组件超过任何其他组件的情况。如上所述，将所有参数设定的单个值α称为浓度参数。如果Dirichlet分布的样本空间被解释为离散概率分布，则直观地，浓度参数可以被认为是确定来自Dirichlet分布的样本的概率质量可能如何“集中”。价值远小于1，质量将高度集中在几个组件中，其余的几乎没有质量。在大于1的值下，质量将几乎平均分散在所有组件中。

弦切Dirichlet分布的一个例子是如果想将字符串（每个初始长度为1.0）切割成具有不同长度的K个片段，其中每个片段具有指定的平均长度，但允许片段的相对大小的一些变化。 α/α0值指定由分布产生的切片的平均长度。该平均值的变化与α0成反比。6

狄利克雷原理在数学中，狄利克雷原理(Dirichlet principle)是将求解拉普拉斯方程狄利克雷问题化为变分问题的方法，所用到的积分称为狄利克雷积分。狄利克雷原理古典形式称，在∂G充分光滑时，只要求分块连续可微的诸函数中，存在使狄利克雷积分达到极小者。自19世纪50年代狄利克雷(Dirichlet，P.G.L.)、黎曼(Riemann，(G.F.)B.)提出该原理之后的半个多世纪，包括希尔伯特(Hilbert，D.)、外尔斯特拉斯(Weierstrass，K.(T.W.))在内的大批数学家为该理论的充实付出了巨大努力。20世纪50年代，戴尼(Deny，J.)用广义函数论的方法把研究深入一步；布雷洛(Brélot，M.E.)把上述结果推广到E空间的区域上去。

狄利克雷原理也就是组合数学里的抽屉原理。