历史发展泰勒简介
18世纪早期 英国牛顿学派最优秀代表人物之一的英国数学家泰勒(Brook Taylor), 于1685 年8月18日在英格兰德尔塞克斯郡的 埃德蒙顿市出生。1701年,泰勒进 剑桥大学的圣约翰学院学习。1709年后移居 伦敦,获得法学学士学位。1712年当选为 英国皇家学会会员,同年进入促裁牛顿和莱布尼兹发明微积分优先权争论的委员会。并于两年后获法学博士学位。从1714年起担任皇家学会第一秘书,1718年以健康为由辞去这一职务。1717年,他以泰勒定理求解了数值方程。最后在1731年1 2月29日于 伦敦逝世。
泰勒以微积分学中将 函数展开成无穷 级数的定理著称于世。这条定理大致可以叙述为:函数在一个点的邻域内的值可以用函数在该点的值及各阶 导数值组成的无穷级数表示出来。然而,在半个世纪里,数学家们并没有认识到泰勒定理的重大价值。这一重大价值是后来由 拉格朗日发现的,他把这一定理刻画为微积分的基本定理。泰勒定理的严格证明是在定理诞生一个世纪之后,由柯西给出的。
泰勒定理开创了有限差分理论,使任何单变量函数都可展成 幂级数;同时亦使 泰勒成了有限差分理论的奠基者。泰勒于书中还讨论了 微积分对一系列物理问题之应用,其中以有关弦的横向振动之结果尤为重要。他透过求解方程导出了基本频率公式,开创了研究弦振问题之先河。此外,此书还包括了他于数学上之其他创造性工作,如论述常 微分方程的奇异解,曲率问题之研究等。1
发展过程希腊哲学家芝诺在考虑利用无穷级数求和来得到有限结果的问题时,得出不可能的结论-芝诺悖论,这些悖论中最著名的两个是“阿喀琉斯追乌龟”和“飞矢不动”。
后来,亚里士多德对芝诺悖论在哲学上进行了反驳,直到德谟克利特以及后来的阿基米德进行研究,此部分数学内容才得到解决。阿基米德应用穷举法使得一个无穷级数能够被逐步的细分,得到了有限的结果。
14世纪,玛达瓦发现了一些特殊函数,包括正弦、余弦、正切、反正切等三角函数的泰勒级数。
17世纪,詹姆斯·格雷果里同样继续着这方面的研究,并且发表了若干麦克劳林级数。直到1712年,英国牛顿学派最优秀代表人物之一的数学家泰勒提出了一个通用的方法,这就是为人们所熟知的泰勒级数;爱丁堡大学的科林·麦克劳林教授发现了泰勒级数的特例,称为麦克劳林级数。1
公式形式泰勒公式泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。
若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶导数,且在开区间(a,b)上具有(n+1)阶导数,则对闭区间[a,b]上任意一点x,成立下式:
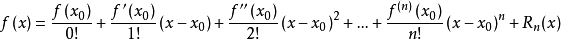
其中,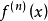 表示f(x)的n阶导数,等号后的多项式称为函数f(x)在x0处的泰勒展开式,剩余的Rn(x)是泰勒公式的余项,是(x-x0)n的高阶无穷小。1
表示f(x)的n阶导数,等号后的多项式称为函数f(x)在x0处的泰勒展开式,剩余的Rn(x)是泰勒公式的余项,是(x-x0)n的高阶无穷小。1
余项泰勒公式的余项Rn(x)可以写成以下几种不同的形式:
1、佩亚诺(Peano)余项:
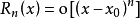
这里只需要n阶导数存在
2、施勒米尔希-罗什(Schlomilch-Roche)余项:
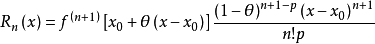
其中θ∈(0,1),p为任意正实数。(注意到p=n+1与p=1分别对应拉格朗日余项与柯西余项)2
3、拉格朗日(Lagrange)余项: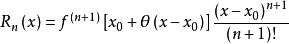
其中θ∈(0,1)。
4、柯西(Cauchy)余项:
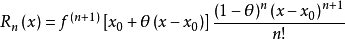
其中θ∈(0,1)。
5、积分余项:
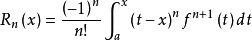
其中以上诸多余项事实上很多是等价的。2
带佩亚诺余项以下列举一些常用函数的泰勒公式1:
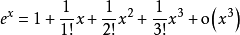
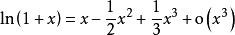
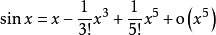
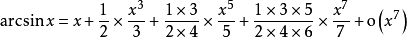
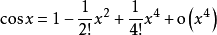
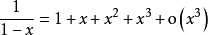
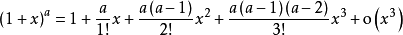
验证推导公式推导我们知道,根据拉格朗日中值定理导出的有限增量定理有:
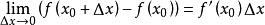
于是:
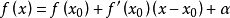
其中误差α是在Δx→0即x→x0的前提下才趋向于0,所以在近似计算中往往不够精确。于是我们需要一个能够足够精确的且能估计出误差的多项式:

来近似地表示函数f(x)且要写出其误差f(x)-P(x)的具体表达式。设函数P(x)满足 :
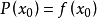
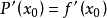
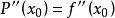
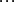
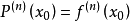
于是可以依次求出A0、A1、A2、……、An,显然有:
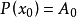 ,所以
,所以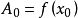 ;
;
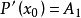 ,所以
,所以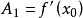 ;
;
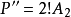 ,所以
,所以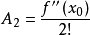 ;
;
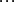
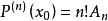 ,所以
,所以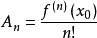 ;
;
至此,多项的各项系数都已求出,得:
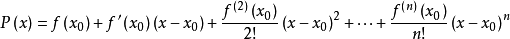
以上就是函数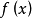 的泰勒展开式。
的泰勒展开式。
接下来就要求误差的具体表达式了。设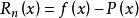 ,令
,令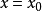 得到:
得到:
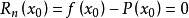
进而:
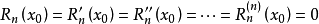
根据柯西中值定理:
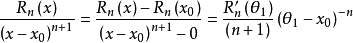
其中θ1在x和x0之间;
继续使用柯西中值定理得到: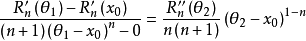
其中θ2在θ1和x0之间;
连续使用n+1次后得到:
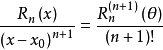
其中θ在x和x0之间;
同时:
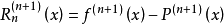
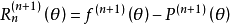
而: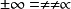
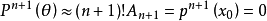
进而:
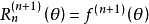
综上可得:
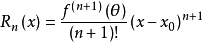
一般来说展开函数时都是为了计算的需要,故x往往要取一个定值,此时也可把Rn(x)写为Rn。1
麦克劳林展开函数的麦克劳林展开指上面泰勒公式中x0取0的情况,即是泰勒公式的特殊形式,若f(x)在x=0处n阶连续可导,则下式成立:
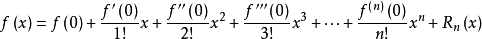
其中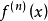 表示f(x)的n阶导数。
表示f(x)的n阶导数。
当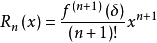 ,其中δ在0与x之间时,公式称为拉格朗日型余项的n阶麦克劳林公式;
,其中δ在0与x之间时,公式称为拉格朗日型余项的n阶麦克劳林公式;
当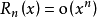 时公式称为带佩亚诺型余项的n阶麦克劳林公式。1
时公式称为带佩亚诺型余项的n阶麦克劳林公式。1
θ的性质n阶泰勒公式中的余项写成如下形式的拉格朗日余项:
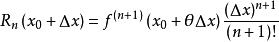
那么其中的θ的有一个重要性质:当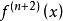 在
在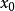 点连续,且
点连续,且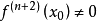 ,则
,则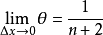 。
。
证明 因为
(1)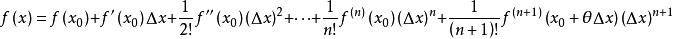 ,
,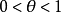 。
。
(2)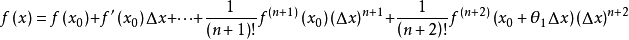 ,
,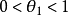 。
。
(3)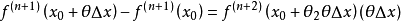 ,
,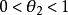 。
。
[(1)-(2)](n+1)!/[(△x)^(n+1)]得:
(4)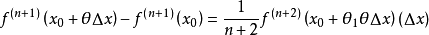 。
。
(3)/(4)得
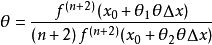
由于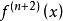 在
在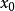 点连续,且
点连续,且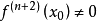 ,所以
,所以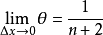 。1
。1
公式应用实际应用中,泰勒公式需要截断,只取有限项,一个函数的有限项的泰勒级数叫做泰勒展开式。泰勒公式的余项可以用于估算这种近似的误差。
泰勒展开式的重要性体现在以下五个方面:
幂级数的求导和积分可以逐项进行,因此求和函数相对比较容易。
一个解析函数可被延伸为一个定义在复平面上的一个开片上的解析函数,并使得复分析这种手法可行。
泰勒级数可以用来近似计算函数的值,并估计误差。
证明不等式。
求待定式的极限。1
实例
例1、展开三角函数y=sinx和y=cosx。
解:根据导数表得:
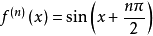
显然y=sinx在x=0处具有任意阶导数,并且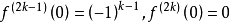 。
。
根据麦克劳林公式:
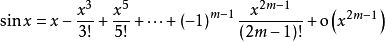
类似地,可以展开y=cosx。
例2、当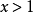 时,证明
时,证明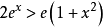 。
。
证明 :函数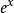 在
在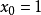 点处的二阶泰勒公式为
点处的二阶泰勒公式为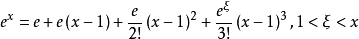
在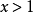 时,显然成立
时,显然成立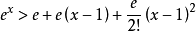 ,即
,即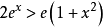 。
。
例3、求极限 。
。
解: 利用
(1)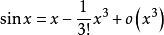 ;
;
(2)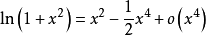 ;
;
(3)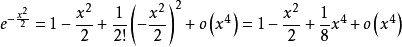 ;
;
(4)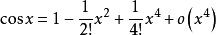 ;
;
可得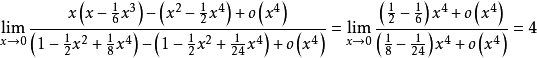 。
。
**例4、**计算近似值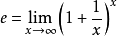 ,并估计误差。
,并估计误差。
解:对指数函数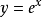 运用麦克劳林展开式并舍弃余项:
运用麦克劳林展开式并舍弃余项:
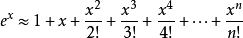
当x=1时:
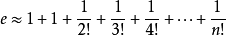
取n=10,即可算出近似值e≈2.7182818。
误差为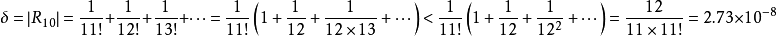
例5、欧拉公式: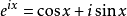
(其中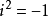 ,即一个虚数单位)
,即一个虚数单位)
证明:
由于在实数范围以内,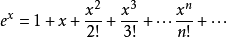
将该式子扩展到复数系内以定义指数函数,得到
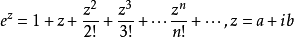
特别地,当上式z=ib时,有
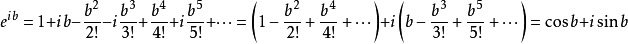
把上面的b换成x,就得到了欧拉公式。
由欧拉公式,对任意一个复数z=a+ib,有
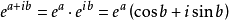
即复数z的指数函数依然是一个复数,这个复数的模r=ea,幅角θ=b。
若b=0,则ez=ea(cos0+isin0)=ea(1+0)=ea,与实变函数f(x)=ex在x=a时的函数值相同。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国