定义
设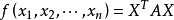 ,其中矩阵
,其中矩阵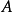 是对称阵,即
是对称阵,即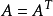 ,
,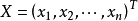 为列向量,若
为列向量,若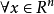 ,
,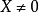 ,有
,有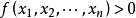 ,则称
,则称 为正定二次型,称实对称矩阵
为正定二次型,称实对称矩阵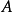 正定。1
正定。1
例如,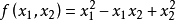 即为正定二次型,其中
即为正定二次型,其中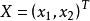 ,
,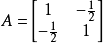 。
。
性质(1) 阶实对称矩阵
阶实对称矩阵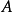 正定
正定
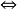
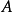 的正惯性指数等于
的正惯性指数等于
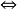
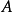 与单位矩阵合同
与单位矩阵合同
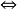
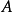 的顺序主子式大于零
的顺序主子式大于零
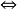
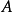 的特征值大于零
的特征值大于零
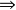
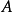 的行列式大于零(但行列式大于零的矩阵不一定是正定矩阵)
的行列式大于零(但行列式大于零的矩阵不一定是正定矩阵)
(2)若 阶实对称矩阵
阶实对称矩阵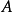 和
和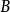 正定,
正定,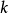 为实数,则
为实数,则
①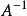 (逆)、
(逆)、 (伴随矩阵)、
(伴随矩阵)、 均正定;
均正定;
②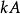 正定
正定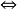
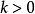 ;
;
③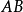 正定
正定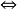
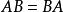
判定方法判定二次型(或对称矩阵)为正定的方法有如下两种
行列式法对于给定的二次型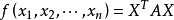 ,写出它的矩阵,根据对称矩阵的所有顺序主子式是否全大于零来判定二次型 (或对称矩阵)的正定性。
,写出它的矩阵,根据对称矩阵的所有顺序主子式是否全大于零来判定二次型 (或对称矩阵)的正定性。
正惯性指数法对于给定的二次型 ,先将化为标准形,然后根据标准形中平方项系数为正的个数是否等于 来判定二次型的正定性。
来判定二次型的正定性。
通过正交变换,将二次型化为标准形后,标准形中平方项的系数就是二次型矩阵的特征值。因此,可先求二次型矩阵的特征值,然后根据大于零的特征值个数是否等于 来判定二次型的正定性。2
来判定二次型的正定性。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国