一般形式
二次规划的一般形式可以表示为:
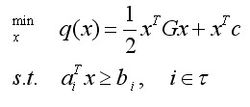
其中G是Hessian矩阵,τ是有限指标集,c,x和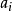 ,都是R中的向量。如果Hessian矩阵是半正定的,则我们说该式是一个凸二次规划,在这种情况下该问题的困难程度类似于线性规划。如果有至少一个向量满足约束并且在可行域有下界,则凸二次规划问题就有一个全局最小值。如果是正定的,则这类二次规划为严格的凸二次规划,那么全局最小值就是唯一的。如果是一个不定矩阵,则为非凸二次规划,这类二次规划更有挑战性,因为它们有多个平稳点和局部极小值点。
,都是R中的向量。如果Hessian矩阵是半正定的,则我们说该式是一个凸二次规划,在这种情况下该问题的困难程度类似于线性规划。如果有至少一个向量满足约束并且在可行域有下界,则凸二次规划问题就有一个全局最小值。如果是正定的,则这类二次规划为严格的凸二次规划,那么全局最小值就是唯一的。如果是一个不定矩阵,则为非凸二次规划,这类二次规划更有挑战性,因为它们有多个平稳点和局部极小值点。
解法到目前为止,已经出现了很多求解二次规划问题的算法,如拉格朗日方法、Lemke方法、内点法、有效集法、椭球算法等等,并且现在仍有很多学者在从事这方面的研究工作。
在数学规划中,由于凸二次规划有着特殊作用,人们一直把它作为一个重要课题加以研究。等式约束二次规划问题的一个求解方法是拉格朗日算法。首先定义拉格朗日函数,对此函数求导,再令导数为零,这样便得到一个线性方程组。拉格朗日算法有两个不足之处:
(1)构造的线性方程组的方程个数与m有关(n+m个方程),当n与m都很大时,将占用计算机很大的存储空间,并且使计算量增加;
(2)必须计算矩阵的逆。
有效集法求解一般凸二次规划问题理论基础首先引入下面的定理,它是有效集方法理论基础1。
设x*是一般凸二次规划问题的全局极小点,且在x*处的有效集为
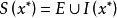
则x*也是下列等式约束凸二次规划:
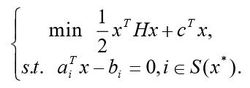
的全局最小点。
从上述定理可以发现,有效集方法的最大难点是事先一般不知道有效集S(x*),因此只有想办法构造一个集合序列去逼近它,即从初始点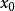 出发,计算有效集
出发,计算有效集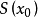 ,解对应的等式约束子问题。
,解对应的等式约束子问题。
修正后的子问题如下:

由此可知,修正后的子问题的全局极小点必然是原问题的一个下降可行方向。
算法步骤有效集方法的算法步骤如下:
(1)选取初值。给定初始可行点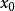 ,令k:=0。
,令k:=0。
(2)解子问题。确定相应的有效集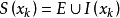
求解子问题
得极小点 和拉格朗日乘子向量
和拉格朗日乘子向量 。若
。若 转步骤(4);否则,转步骤(3)。
转步骤(4);否则,转步骤(3)。
(3)检验终止准则。计算拉格朗日乘子:
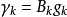
其中
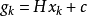
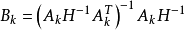
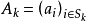
令
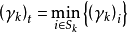
若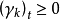 ,则
,则 是全局极小点,停算;否则,转步骤(2)。
是全局极小点,停算;否则,转步骤(2)。
(4)确定步长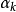 。令
。令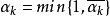 ,其中
,其中

令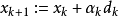 。
。
(5)若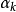 =1,则令
=1,则令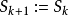 ;否则,若
;否则,若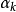




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国