[科普中国]-主曲率

简介

过曲面上某个点上具有无穷个正交曲率，其中存在一条曲线使得该曲线的曲率为极大，这个曲率为极大值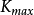 ，垂直于极大曲率面的曲率为极小值 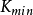。这两个曲率属性为主曲率。他们代表着法曲率的极值。

曲率的分类平均曲率、主曲率和高斯曲率是曲率的三个基本要素。

主曲率和主方向对曲面S : r = r(u, v)上一给定点P0(u0, v0)，法曲率kn是切方向du : dv的函数，称法曲率的每个临界值(critical value)为曲面在这一点的主曲率；对应的方向称为曲面在这一点的主方向。1

定理定理1曲面在非脐点处，两个主方向互相垂直。2

定理2曲面上一点由方程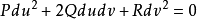 所确定的两个切方向互相垂直的充要条件是 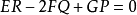，这里E、F、G是曲面的第一类基本量。

证明：两个方向du:dv和δu:δv 正交的充要条件是

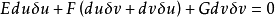
换一种写法即

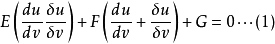
将已知的二次方程写成

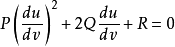
将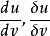 是它的两个根，且均应满足上述方程，由根与系数的关系知

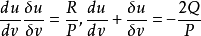
将上式代入式（1）即得引理。

定理3曲面在非脐点处的主曲率是曲面在这点沿所有方向的法曲率中的最大值和最小值。

证明：设k1、k2 是两个主曲率，不妨设k1 0，双曲点处K