[科普中国]-解析数论

简介

数论中以分析方法作为研究工具的一个分支。分析方法在数论中的应用可以追溯到18世纪L.欧拉的时代。欧拉证明了，对实变数s>1有恒等式 （式中s取遍所有素数）成立，并且由此推出素数有无穷多个。欧拉恒等式是数论中最主要的定理之一。随后P.G.L.狄利克雷创立了研究数论问题的两个重要工具，即狄利克雷（剩余）特征标与狄利克雷L函数，奠定了解析数论的基础。

解析数论是在初等数论无法解决的情况下发展起来的，因为，如果有了一个可以表达所有素数的素数普遍公式，一些由解析数论范围的内容，就自动转到初等数论的范围内。例如孪生素数猜想以及哥德巴赫猜想。

联系数论和复变函数论的桥梁是所谓的佩隆公式(Peron)。很多数论问题可以归结为某类求和函数的估计问题，而利用佩隆公式，就可以将求和函数的估计转变为某类复变函数的零点、极点的分布情况的估计。 大多数数论问题最终都能归结为L函数的性质讨论。

令π（x）表示不超过x的素数的个数，关于π（x）的研究是素数论的中心问题，黎曼在数论中引入复变函数ζ(s)，称为黎曼ζ函数（见数论），他对这个函数作了深入的研究，得到了许多重要结果。特别是 ，他建立了一个与ζ（s）的零点有关的表示π(x）的公式，因此研究素数分布问题的关键在于研究ζ（s）的性质特别是它的零点的性质。这样，黎曼开创了解析数论的一个新时期。黎曼提出一个猜想：ζ(s)的所有复零点都在直线Res=1/2上，这就是所谓黎曼猜想。它是尚未解决的最著名的数学问题之一。

1896年，J.阿达马与C.J.dela瓦莱-普桑用解析方法同时并且相互独立地证明了素数定理即当x→∞时，π（x）～.x/lnx （这个问题最早由高斯提出），从此解析数论开始得到迅速发展。1949年，A.塞尔伯格与P.爱尔特希分别给出了对于素数定理的一个十分初等的分析证明，当然它是很复杂的。

解析数论起源于素数分布、哥德巴赫猜想、华林问题以及格点问题的研究、解析数论的方法主要有复变积分法、圆法、筛法、指数和方法、特征和方法、密率等。1

解析数论的基础欧拉恒等式是数论中最重要的定理之一，是算术基本定理的解析等价形式，揭示了素数p和自然数n之间的积性关系。他还提出了母函数法，利用幂级数来研究整数分拆，这导致圆法和指数和方法的产生。其后，P.G.L.狄利克雷应用分析方法于1837年解决了首项与公差互素的算术级数中有无限多个素数的问题，又于1839年推证出二次域的类数公式。他创立了研究数论的两个重要工具，即狄利克雷(剩余)特征标与狄利克雷l函数，奠定了解析数论的基础。

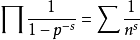1859年，（G.F.）B.黎曼发表了一篇关于不大于x的素数个数π(x)的著名论文《论不大于一个给定值的素数个数》，这是他在数论方面公开发表的惟一的文章。他把恒等式的右边的级数记作ζ(s)，所不同之处是把s看作复变数。现在称ζ(s)为黎曼ζ函数。他认为素数性质可以通过复变函数ζ(s)来探讨，并对复变函数ζ(s)做了深刻的研究，得到许多重要结果。特别是他建立了一个与ζ(s)的零点有关的表示π(x)的公式。因此研究素数分布的关键在于研究复变函数 ζ(s)的性质,特别是ζ(s)的零点性质。这一杰出的工作，是复变函数论的思想和方法应用于数论研究的结果。黎曼开创了解析数论的新时期，也推动了单复变函数论的发展。在文章中他提出了一个猜想：ζ(s)的所有复零点都在直线 Res=1/2上。这就是所谓黎曼猜想。它是至今没有解决的最著名的数学问题之一。它的研究对解析数论和代数数论的发展都有极其深刻的影响。1

解析数论的发展1896年，J.（-S.）阿达马与C.de la瓦莱-普桑严格地按照黎曼提出的方法和结果，用整函数理论，同时证明了素数定理：当x→∞时,π(x)～x(lnx)-1。从此解析数论开始得到迅速发展，而在此以前的30年中却无显著进展。 在数论中应用分析方法，大致有两种情况：一是数论问题本身不涉及分析概念。这类问题又可分为两种情形，或者有一些问题不应用分析方法就不能解决，例如，上述的狄利克雷的两个工作、三素数定理（见数论、堆垒数论）、华林问题；或者有一些问题应用分析方法可使证明简单、可以对问题做定量研究，例如，应用母函数法对整数分拆的一些恒等式的证明、欧拉证明素数有无穷多个的分析方法导致H.默滕斯证明了关于素数平均分布的三个定理、堆垒数论的许多问题引入分析方法证明解的存在性，得出解数的渐近公式或上下界估计。二是数论问题本身必须用分析概念才能表达清楚。例如，关于素数定理,即不大于x的素数个数π(x)等于多少的问题（见素数分布）。此外，利用分析概念还可提出新的数论问题，例如各种数论函数的阶估计及均值估计（见格点问题）。

解决一个数论问题需要用到多深的分析工具，或者能否不用分析工具。这也是数学家努力为之探索的问题。例如，在1949年A.赛尔伯格与P.爱尔特希不利用ζ函数，且除了极限、ex和lnx的性质外,也不需要其他的分析知识，给出了素数定理一个十分初等的分析证明。当然它是很复杂的。

解析数论起源于素数分布、哥德巴赫猜想、华林问题以及格点问题的研究。解析数论的方法主要有复变积分法、圆法、筛法、指数和方法、特征和方法、密率等。模形式论与解析数论有密切关系。1

解析数论两大问题解析数论，一直以来有两大问题，素数方程与L-函数。

素数方程素数，即我们中小学学到的质数，从乘法角度讲，相当于构成整数的“原子”。Goldbach猜想，即是一种素数方程问题，即方程的解集在素数集合里考虑。

Fields奖得主Bombieri在大筛法方面做出了重要工作，从而给陈景润等一批中国数学家带来机会，先是潘承洞解决了1+5型问题，王元解决2+3型的同时构造出了后续攻击路线的解决框架，包括1+4和1+3，最后由陈景润解决了1+2型问题，一直到现在都无法改进，是中国数学家目前为止最拿得响的工作，因为目前谁也做不出最难的1+1型。

素数方程方面，1998年Fields奖得主Gowers获奖之后，紧接着在整数方程做出了开创性的工作，然后由Terence Tao（陶哲轩）和Ben Green推广到素数方程方面，这个推广，很不平凡，陶哲轩获得了2006年Fields奖。

Gowers-Tao-Green的思想，将素数方程做了系统的突破，可以解决绝大多数的线性方程组问题，唯独不能攻击Goldbach猜想。

素数方程方面，一直以来有两大方法：筛法和圆法。前者自古希腊时期就被发现，陈景润的工作，就是动用此法。圆法，则是英国剑桥的Hardy-Littlewood-Ramanujan发明，至今也应用了90多年了。

Gowers-Tao-Green，其价值地位相当于第三种方法出世，正是因为增加了新的理解，才有可能得到新的突破性结果。Gowers-Tao-Green增加的是哪种新思想，这种新思想，除了素数方程的数论问题之外，亦很可能对其他数学领域也产生深刻影响。

经典解析数论在素数方程方面的研究思路是：

A-Step 1. Summation Formulas (各种求和公式)

A-Step 2. Equations Detect (方程探测)

L-函数一般地说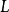， -函数来源由两类组成：算术L-函数和自守L-函数。这两者又是密切联系在一起的，根据罗伯特·朗兰兹的猜想，笼统地说， 一切有意义的L-函数都来自自守L-函数。

算术L-函数

简单地说，

同样地，狄利克雷在研究算术级数中的素数分布时，引入了Dirichlet L-函数：

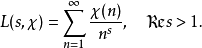
Dedekind zeta-函数：设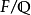 为一代数数域，

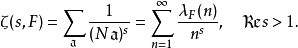
椭圆曲线的Haass-Weil L-函数：设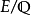 为一非奇异的椭圆曲线 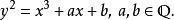定义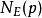 为曲线在有限域 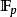上的解，设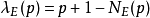 ，则下面的级数称为关于曲线的Haass-Weil L-函数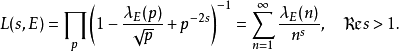

阿廷L-函数：设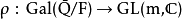 是一个有限维的伽罗瓦表示，其中 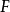为一代数数域，

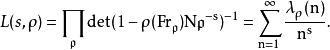
自守L-函数

全纯模形式的L-函数，Maass L-函数，标准L-函数等等。

研究内容

根据罗伯特·朗兰兹在国际数学家大会上的报告所指，研究一个L-函数主要有三部分内容：

1.解析延拓

L-函数的解析延拓和函数方程这是最基本的一部分。对于一般的自守L-函数这是较容易得到的， 但是对算术的L-函数这一部分并不是容易得到的。例如，对于Haass-Weil L-函数，这部分就是谷山-志村猜想，该猜想一部分就能推出费尔马大定理。关于阿廷L-函数的全纯解析沿拓的阿廷猜想也是数论中重要的未知问题。

对于数学对象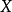 的L-函数，我们定义其的gamma因子为2

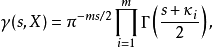
其中 为复参数。

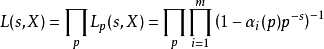
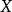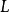定义下面关于 的完全 -函数

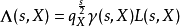
那么，一般地我们有函数方程

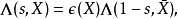
其中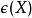 为模为1的复数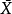， 为关于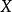 的对偶对象。

2.零点的分布

非零区域：如黎曼zeta函数的目前最好的非零区域为

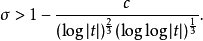
黎曼猜想和广义黎曼猜想问题：

在假设黎曼猜想下，零点虚部的分布问题与随机矩阵的联系等等。

3.特殊点的值

中心值，临界点，整点的值，极点的留数等。这里面也有很多猜想，像BSD猜想，类数问题，Deligne 猜想，Beilinson 猜想，Goldfeld猜想。其实往往我们重要的不仅是关心它具体有多大，而是关心的这个量里面隐含着什么样的算术意义。像Dedekind zeta 函数在s=1处的留数，里面包含了一个数域的很多不变量：类数，判别式，regular等；BSD猜想就是Haass-Weil L-函数在中心点的的阶就是该椭圆曲线的秩！3