简介
最小距离分类法是分类器里面最基本的一种分类方法,它是通过求出未知类别向量X到事先已知的各类别(如A,B,C等等)中心向量的距离D,然后将待分类的向量X归结为这些距离中最小的那一类的分类方法。1
基本原理在一个n维空间中,最小距离分类法首先计算每一个已知类别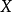 (用向量表示是
(用向量表示是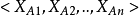 )的各个维度的均值,形成一个均值
)的各个维度的均值,形成一个均值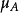 ,用向量表示
,用向量表示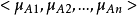 )(A为类别的名称,
)(A为类别的名称,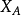 是类别A的样本特征集合,
是类别A的样本特征集合,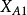 是类别A的第1维特征集合,
是类别A的第1维特征集合,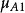 是第一维特征集合的均值,n为总的特征维数),同理,计算另一个类别
是第一维特征集合的均值,n为总的特征维数),同理,计算另一个类别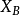 (用向量表示是
(用向量表示是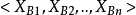 )的均值
)的均值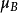 ,用向量表示
,用向量表示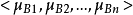 ,那么对于一个待分类的样本特征向量x(用向量表示是
,那么对于一个待分类的样本特征向量x(用向量表示是 ),怎么判断它是属于类别
),怎么判断它是属于类别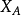 ,还是
,还是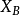 呢?我们只需要分别计算到
呢?我们只需要分别计算到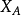 和
和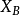 的距离
的距离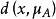 和
和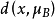 ,以欧式距离为例,距离的计算公式如下:
,以欧式距离为例,距离的计算公式如下:
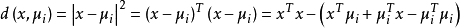
然后找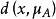 和
和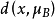 中的最小值,如果前者最小,那么X属于A类,如果后者小,那么X属于B类。
中的最小值,如果前者最小,那么X属于A类,如果后者小,那么X属于B类。
分类器的距离目前有多种不同的计算分类距离的方法,在上面的距离计算公式中,是我们最常见的计算距离的方法,欧氏距离。另外也有其它很多的距离公式,如欧氏距离,曼哈顿距离,闵可夫斯基距离,切比雪夫距离,标准化欧式距离等等,这里不一一做介绍,只对下面的三个距离做重点介绍一下,以是我们能够理解不同距离,对应不同的意义23:
欧氏距离欧氏距离(EuclideanDistance)是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式。
(1)二维平面上两点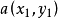 与
与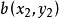 间的欧氏距离:
间的欧氏距离:
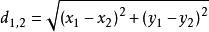
(2)三维空间两点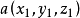 与
与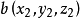 间的欧氏距离:
间的欧氏距离:
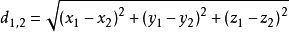
3)两个n维向量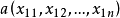 与
与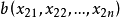 间的欧氏距离:
间的欧氏距离:
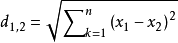
曼哈顿距离从名字就可以猜出这种距离的计算方法了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源, 曼哈顿距离也称为城市街区距离(City Blockdistance)。
(1)二维平面两点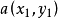 与
与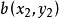 间的曼哈顿距离:
间的曼哈顿距离:
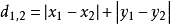
(2)两个n维向量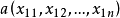 与
与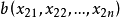 间的曼哈顿距离:
间的曼哈顿距离:
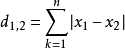
闵可夫斯基距离闵氏距离(MinkowskiDistance)不是一种距离,而是一组距离的定义。
(1)闵氏距离的定义
两个n维变量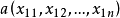 与
与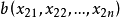 间的闵可夫斯基距离定义为:
间的闵可夫斯基距离定义为:

其中p是一个变参数。
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
p取不同的值,公式也不一样,所以随着参数p的不同,闵氏距离可以表示一类的距离。
最小距离分类的步骤最小距离分类器的步骤,其实是我们做监督分类基本的几个步骤。
(1)确定类别m,并提取每一类所对应的已知的样本。
(2)从样本中提取出一些可以作为区分不同类别的特性,也就是我们通常所说的特征提取,如果提取出了n个不同的特性,那么我们就叫它n维空间,特征提取对分类的精度有重大的影响。
(3)分别计算每一个类别的样本所对应的特征,每一类的每一维都有特征集合,通过集合,可以计算出一个均值,也就是特征中心。
(4)通常为了消除不同特征因为量纲不同的影响,我们对每一维的特征,需要做一个归一化,或者是放缩到(-1,1)等区间,使其去量纲化。
(5)利用选取的距离准则,对待分类的本进行判定。
优点和缺点最小距离分类法原理简单,容易理解,计算速度快,但是因为其只考虑每一类样本的均值,而不用管类别内部的方差(每一类样本的分布),也不用考虑类别之间的协方差(类别和类别之间的相关关系),所以分类精度不高,因此,一般不用它作为我们分类对精度有高要求的分类,但它可以在快速浏览分类概况中使用。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国