定义
以 为横轴,以麦克斯韦分布函数
为横轴,以麦克斯韦分布函数 为纵轴,画出的图线叫做麦克斯韦速率分布曲线(如图所示),它能形象地表示出气体分子按速率分布的情况。图中任一区间
为纵轴,画出的图线叫做麦克斯韦速率分布曲线(如图所示),它能形象地表示出气体分子按速率分布的情况。图中任一区间 内曲线下的窄条面积表示在该区间内的分子数占总分子数的比率
内曲线下的窄条面积表示在该区间内的分子数占总分子数的比率 ,而任一有限范围
,而任一有限范围 内曲线下的面积则表示分布在这范围内的分子所占的比率
内曲线下的面积则表示分布在这范围内的分子所占的比率

曲线分析由上图可见速率分布曲线从坐标原点出发,经过一极大值后,随速率的增大而渐近于横坐标轴。这说明,气体分子的速率可以取由0到 之间的一切数值,速率很大和很小的分子所占的比率实际上都很小,而具有中等速率的分子所占的比率却很大。与
之间的一切数值,速率很大和很小的分子所占的比率实际上都很小,而具有中等速率的分子所占的比率却很大。与 极大值对应的速率叫做最概然速率,通常用
极大值对应的速率叫做最概然速率,通常用 表示。它的物理意义是,如果把整个速率范围分成许多相等的小区间,则分布在
表示。它的物理意义是,如果把整个速率范围分成许多相等的小区间,则分布在 所在的区间的分子比率最大。于是有
所在的区间的分子比率最大。于是有

由此得
 (1)
(1)
即温度越高, 越大;分子质量越大,
越大;分子质量越大, 越小。与
越小。与 对应的
对应的 值为
值为
 (2)
(2)
即温度越高, 值越小。
值越小。
麦克斯韦分布函数 表明,对于给定的气体(即
表明,对于给定的气体(即 一定),分布曲线的形状随温度而变。如右图中画出了
一定),分布曲线的形状随温度而变。如右图中画出了 和
和 两个温度的分布曲线。当温度升高时,速率较大的分子加多,
两个温度的分布曲线。当温度升高时,速率较大的分子加多,
 最概然速率
最概然速率 变大,所以曲线的高峰移向速率大的一方。但由于曲线下的总面积恒等于1,所以温度升高时曲线变得较为平坦。
变大,所以曲线的高峰移向速率大的一方。但由于曲线下的总面积恒等于1,所以温度升高时曲线变得较为平坦。
在同一温度下,分布曲线因气体不同而异。因为最概然速率 与分子质量的平方根
与分子质量的平方根 成反比,所以大质量分子的
成反比,所以大质量分子的 小,曲线高峰移向速率小的一方。
小,曲线高峰移向速率小的一方。
用麦克斯韦速率分布函数可以求出平衡态下理想气体分子的平均速率。平均速率的定义是

将麦克斯韦速率分布函数代入上式,可得

还可以用速率分布函数求 的平均值。由平均值的定义有
的平均值。由平均值的定义有

将麦克斯韦分布函数代入求解后,并取平方根,可得方均根速率为

由上面的结果可见,气体分子的3种统计平均速率值 和
和 都与
都与 成正比,与
成正比,与 或
或 成反比。其中
成反比。其中 最大,
最大,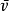 次之,
次之, 最小。在室温下,它们的数量级一般为每秒几百米。3种速率有不同的应用,讨论速率分布时要用到最概然速率
最小。在室温下,它们的数量级一般为每秒几百米。3种速率有不同的应用,讨论速率分布时要用到最概然速率 ;在计算分子的平均平动动能时要用到方均根速率
;在计算分子的平均平动动能时要用到方均根速率 ;以后在计算分子的碰撞频率时,要用到平均速率
;以后在计算分子的碰撞频率时,要用到平均速率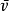 。1
。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国