[科普中国]-幂级数

概念

设 是定义在某区间I上的函数列，则表达式

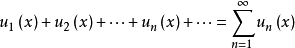(1)

称为定义在区间I上函数项级数。

如果式（1）上的各项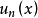 都是定义在区间 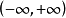上的幂函数，函数项级数 (2)

称作幂级数，其中 为常数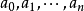， 称为幂级数的系数。

特别的，当 =0时，幂级数式（2）变为

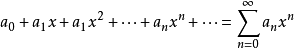(3)

对于定义在区间I上的函数项级数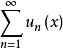 ,取定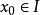 ,就变成数项级数

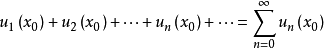(4)

数项级数式（4）可能收敛，也可能发散。如果数项级数式（4）是收敛的，称 为函数项级数（1）的收敛点；如果数项级数式（4）是发散的，称 为函数项级数（1）的发散点。函数项级数式（1）的所有收敛点的集合称为其收敛域，所有发散点的集合称为其发散域。

对于收敛域上的每一个数x，函数项级数（1）都是一个收敛的常数项级数，因而有一确定的和。因此，在收敛域上函数项级数的和是x的函数，称为函数项级数的和函数，记作s（x），通常写成

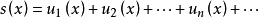或 。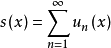

收敛半径和收敛域如果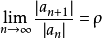 ,则幂级数 的收敛半径R：

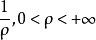
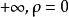
运算四则运算（1）幂级数的加法

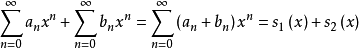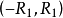在和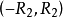中的较小区间内上式成立，收敛半径。

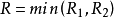（2）幂级数的减法

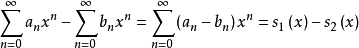
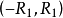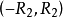在和中的较小区间内上式成立，收敛半径。

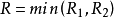（3）幂级数的乘法

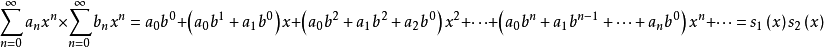
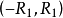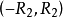在和中的较小区间内上式成立，收敛半径。

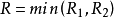(4)幂级数的除法

两个幂级数相除的结果仍是幂级数。假设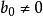时，

系数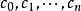由下列等式逐一确立：

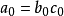
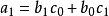
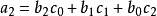
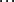
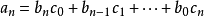
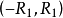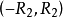相除所得的幂级数的收敛域可能比和小得多。

幂级数的和函数的性质性质一：幂级数的和函数s（x）在其收敛域I上连续。

性质二：幂级数的和函数s（x）在其收敛域I上可积，并有逐项积分公式

逐项积分后所得的幂级数和原级数有相同的收敛半径。

推论：幂级数的和函数s（x）在其收敛域内可逐项积分任意次。

性质三：幂级数的和函数s（x）在其收敛区间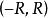内可导，并有逐项求导公式

逐项求导后所得的幂级数和原级数有相同的收敛半径。

推论：幂级数的和函数s（x）在其收敛区间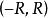内有任意阶导数。1