[科普中国]-分式理想

概念

分式理想(fractional ideal)是比理想更广的一种理想。它由整环的商域中元构成。设K是整环R的商域。若X是R模K的子模，并且存在K中非零元β使得βXR，则称X为R的一个分式理想。有时为了区别，把R的理想称为整理想。整理想都是R的分式理想.若δ1，δ2，…，δn是K中元素，则δ1R+δ2R+…+δnR是R的分式理想，称为由δ1，δ2，…，δn所生成的分式理想。特别地，由K中一个元素δ生成的分式理想δR称为R的主分式理想，也记为(δ)。当a∈R时，主分式理想(a)就是主整理想。1

理想理想是集合论中的基本概念之一。设S为任意集合，若I⊆P(S)且满足：

1.∅∈I;

2.若X，Y∈I，则X∪Y∈I;

3.若X，Y⊆S，X∈I，Y⊆X，则Y∈I;

则称I为集合S上的理想。理想的概念在现代数学的几乎每个分支中均有应用，且有许多变体或引申。例如，布尔代数上的理想即为集合上的理想的一种变体。设B为任意布尔代数，若B的一个子集I满足：

1.0∈I，1∉I(其中0，1分别为布尔代数B中的零元与么元);

2.对任何u∈I，v∈I，有u+v∈I;

3.对任何u，v∈B，若u∈I且v≤u，又v∈I;

则称I为B上的理想。

整环非退化为{0}且没有0因子的交换环称为整环。

环Z是整环。设n为非零自然数；为使环Z/nZ为整环，必须且只须n是素数。任一交换体是整环对任一整环A，系数取自A中含一个未定元的全体多项式之环A[X]，系数取自A中的全体形式级数之环A[[X]]都是整环。由此推知，系数取自交换体K中含p个未定元的全体多项式之环K[X1，X2，…，Xp]及含p个未定元的全体形式级数之环K[[X1，X2，…，Xp]]都是整环。2

商域商域一类特殊且重要的域。包含给定整环的最小域。从整环构作商域的方法类似于由整数环构作有理数域。设R是整环，R°=R\{0}，在卡氏积R×R°中定义等价关系：

(a，b)～(c，d)ad=bc.

将R×R°中元素按等价关系分类，用a/b表示(a，b)所在的等价类.若F是全体等价类的集合，并在F中规定加法和乘法运算：

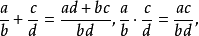
则F构成一个域。而a→aq/q，q∈R°是R到F的一个同构嵌入映射。因此，R可视作F的子环。如此所构造的域F称为R的商域，或称为R的分式域。R中非零元皆为F中可逆元。商域的重要性在于常可通过商域F去研究环R。

模模是一个重要的代数系统。它是一个带算子区A的交换(加)群M。给定集合A与交换群M，若定义了a∈A与x∈M的乘积ax∈M，并且这个积满足条件：

1.a(x+y)=ax+ay (a∈A，x，y∈M)，

则称A为M的算子区，称M为带算子区A的模，又称为A上的模或A模.这时，由对应(a，x)→ax确定的映射A×M→M，称为A作用到M上的运算.任意a∈A可诱导出M的自同态aM：x→ax，而考虑交换群M能否成为A模就是看能否给出映射：

μ： A→End(M)， a→aM.

特别地，考虑A是结合环，若满足上述条件1的A模还满足：

2.(a+b)x=ax+bx;

3.(ab)x=a(bx);

即映射μ：A→End(M)为环同态，则称M为左A模或左环模。由于A到M上的运算是写在左侧，所以M就称为左A模，记为AM。类似地，有右A模M，记为MA.若A有单位元1，且又满足条件：

4.1x=x (x∈M);

则称M为酉模或幺模，以下设A模都是酉模。3