描述
阿基米德公理(又称阿基米德性质),是描述实数之间的大小关系的性质。它与柯西收敛准则共同描述了实数的连续性(即实数与数轴上的点一一对应)。2
这个概念源于古希腊对量的理论;如大卫·希尔伯特的几何公理,有序群、有序域和局部域的理论在现代数学中仍然起着重要的作用。
阿基米德公理可表述为如下的现代记法: 对于任何实数x,存在自然数n有n>x。
在现代实分析中,这不是一个公理。它退却为实数具完备性的结果。基于这理由,常以阿基米德性质的叫法取而代之。
形式叙述解释简单地说,阿基米德性质可以认为以下二句叙述的任一句:2
给出任何数,你总能够挑选出一个整数大过原来的数。
给出任何正数,你总能够挑选出一个整数其倒数小过原来的数。
这等价于说,对于任何正实数a、b,如果 a0时,取N=1即可,故以下证明均假设y>x>0。2
由于阿基米德性质与柯西收敛准则共同反映了实数的连续性,所以可以用实数的连续性公理——戴德金定理来证明二者。
其中柯西收敛准则的证明可参考相应词条,以下只通过戴德金定理来证明阿基米德性质。
反证法:假设不存在这样的正整数N,使Nx>y,即假设对一切正整数n,都有nx≤y。
根据上界的定义,y是数集{nx}的一个上界,这里n=1、2、3、……。取{nx}的所有上界作为集合B,并把B在实数集R中的补集记为A,则:
①显然y∈B,而0∈A,所以A、B都是非空数集——不空
②A∪B=R——不漏
③由取法可知,对B中的任一元素b,都有b≥nx。而因A中的元素都不是{nx}的上界,故对A中的任一元素a,在数集{nx}中存在某个数n0x,满足aξ,那么n0x∈B。
∵n0+1>n0,x>0,由不等式的性质可知(n0+1)x>n0x
但由数集B的定义,数集B中的任何一个元素都不小于nx,这里n=1、2、3、……而(n0+1)x∈{nx},所以属于数集B的n0x也将不小于(n0+1)x,这样一来便产生了矛盾。
∴无论是哪种情况,都有nx≤ξ,n=1、2、3、……
取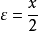 ,则
,则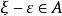
∴存在自然数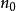 和
和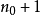 ,满足
,满足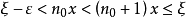
或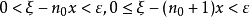
∵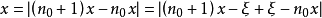
而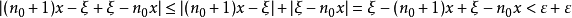
∴有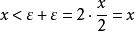 ,矛盾
,矛盾
∴一定存在正整数N,使Nx>y成立,阿基米德性质得证。
推论设a是任一正实数,则存在正整数n,使不等式ay,即n>a。
该推论表示,自然数集N没有上界,即不存在一个数大于所有的自然数。
其他解释欧几里得的解释:
任意给定两个正实数a、b,必存在正整数n,使na>b。
几何描述:在长短不同的两条线段中,无论较长的线段怎样长,较短的线段怎样短,总可以在较长的线段上连续截取较短的线段,并且截到某一次以后,必出现下面两种情况:
1:没有剩余;
2:得到一条短于较短线段的剩余线段。
举例例1:
在一条直线上截取任意两条线段A,B。都符合A+A+A+···+A=A·N>B
这就是“阿基米德公理”有时也叫阿基米德-欧多克斯公理,因为阿基米德把这个命题归功于欧多克斯。其实,比欧多克斯更早些,我国古代《墨经》上已记载着“穷,或有前不容尺也”,指的正是这个意思。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国