[科普中国]-圆外切四边形

性质

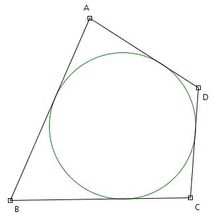
圆的外切四边形的两组对边的和相等。同时，四边形是圆外切四边形的重要条件是四边形的对边和相等.

定理证明可利用切线长定理.

四边形是圆外切四边形的充要条件是该四边形被其对角线所分成的四个小三角形的四个内心共圆.

如图，四边形ABCD外切于00．则AB+CD=AD+BC1．

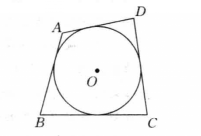
特殊举例圆外切四边形是平行四边形只有两种情况：

1.圆外切菱形

2.圆外切正方形

性质：圆可以外切于一个正 方形，也可以内接于一个正方形

对于圆来说，他与外边的四边形外切，对于四边形来说，他与里边的圆内接.

相关定理(1)圆的外切四边形中，两双对边之和相等．

(2)若四边形两双对边之和相等，则此四边形外切于圆2．