[科普中国]-微分学

概念

建立微分学所用的分析方法对整个数学的发展产生了深远的影响，运用到了许多数学分支中，渗透到自然科学与技术科学等极其众多的领域。微分学的作用是在自然科学中用数学来不仅仅表明状态，并且也表明过程（运动）。微分学的基本思想在于考虑函数在小范围内是否可能用线性函数或多项式函数来任意近似表示。直观上看来，对于能够用线性函数任意近似表示的函数，其图形上任意微小的一段都近似于一段直线。在这样的曲线上，任何一点处都存在一条惟一确定的直线──该点处的“切线”。它在该点处相当小的范围内，可以与曲线密合得难以区分。这种近似，使对复杂函数的研究在局部上得到简化。微分学的基础是建立在实数、函数、极限、连续性等一组基本概念之上的。微分学主要研究以下内容。

导数瞬时速度微分学的核心概念，主要始原于研究如何确定非匀速直线运动质点的瞬时速度与平面曲线上一点处的切线方向。

原是一个纯粹的物理概念。它是在人们经过多次反复观察比较种种非匀速直线运动，尤其在研究物体的碰撞运动而获得大量经验之后产生的。精确科学要求，不仅要准确、清晰而定性地表达这个概念（当然必须与经验的瞬时速度概念相一致），而且要能同时给出确定速度数值的方法。这就促使人们在数学上要建 立一种对函数施加的独特的运算。

设一个非匀速直线运动的质点所行的路程 s与时间t的依赖关系是 s=f(t)。 如果要定义质点在某一给定时刻t的速度(瞬时速度),并计算出这速度的数值，考虑时刻t的一个邻近值t1，在t到t1这段时间Δt=t1-t中，质点运动的路程是 △s=f(t1)-f(t)，从而这段路程上的平均速度是：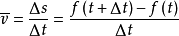

在一般常见的情形，当Δt很小,相应的尌就很接近于时刻t的瞬时速度，而且一般说来，Δt愈小，尌就愈接近于该时刻的瞬时速度。这说明,时刻t的瞬时速度可以表现为路程变化量与时间变化量之比当Δt趋于零（而始终不等于零）时的极限: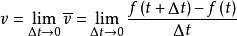。只要这个极限存在，就利用它来定义瞬时速度并计算其数值。

切线方向若质点作曲线运动，则在每一瞬时，运动的特征首先在方向上。对质点运动瞬时方向的数量分析也将导致对函数施加与计算瞬时速度类似的运算。

设一个质点在一平面上运动，其轨迹在取定一个笛卡儿坐标系后可以表示成曲线y=ƒ(x)。如果要考虑怎样确定质点运动到曲线上一任意给定点p（x,y）时的瞬时方向，为此在曲线上取p的一邻近点Q(x1,y1)。很容易看到割线pQ的方向近似于质点在p处的瞬时方向,而且一般说来，x1愈接近x，近似程度就愈好。如果当Q沿曲线趋近p,割线pQ趋近某个极限位置pT，则占据这个极限位置的直线就称为曲线在点p处的切线，这切线的方向就是运动质点在点p处的瞬时方向。切线pT与.横轴的夹角θ,就应当是割线pQ与横轴夹角φ的极限。因此切线pT的斜率k=tanθ可以如下计算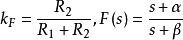：。若令Δx=x1-x，则有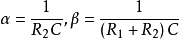。只要这个极限存在,就决定了曲线y=ƒ(x)在点p(x,y)处的切线的方向。

定义导数也称微商。上述两个问题尽管有着不同的物理方面或几何方面的背景，但在数量关系上并没有区别,解决问题所涉及的运算也是相同的:从自变量x的变化量Δx出发，求出相应的因变量y的变化量Δy以后，取商Δy/Δx，再令Δx趋于零(而始终不等于零)取极限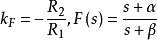。这个极限运算称为函数的微分运算，运算的结果称为函数的导数。

准确地说，函数y=ƒ(x)在给定一点x处的导数定义为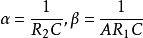。这里说的是这个极限存在的情况，这时又称函数ƒ(x)在点x处是可微的。如果这个极限不存在,就认为ƒ(x)在x处没有导数,并称ƒ(x)在点x处不可微。例如ƒ(x)=|x|在x=0处就是不可微的。容易看出,如果因变量的变化量Δy=ƒ(x+Δx)-ƒ(x)不随Δx趋于零,则上述极限不会存

在，所以函数在其不连续点处一定是不可微的。值得注意的是,函数在其连续点处也有可能是不可微的,如前面所给出的例ƒ(x)=|x|就在x=0处连续而不可微。K.（T.W.）外尔斯特拉斯曾给出一个例子(1872)，其中的函数处处连续但处处不可微。所以，函数的可微性要求比连续性强得多。外尔斯特拉斯给出的函数是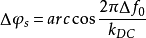式中0