起源
牛顿法最初由艾萨克·牛顿在《流数法》(Method of Fluxions,1671年完成,在牛顿去世后的1736年公开发表)中提出。约瑟夫·鲍易也曾于1690年在Analysis Aequationum中提出此方法。
原理把非线性函数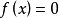 在
在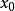 处展开成泰勒级数
处展开成泰勒级数
 取其线性部分,作为非线性方程的近似方程,2则有
取其线性部分,作为非线性方程的近似方程,2则有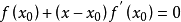
设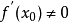 ,则其解为
,则其解为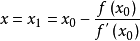
因为这是利用泰勒公式的一阶展开,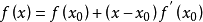 处并不是完全相等,而是近似相等,这里求得的
处并不是完全相等,而是近似相等,这里求得的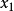 并不能让
并不能让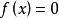 ,只能说
,只能说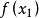 的值比
的值比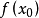 更接近
更接近 ,于是乎,迭代求解的想法就很自然了,
,于是乎,迭代求解的想法就很自然了,
再把f(x)在x1 处展开为泰勒级数,取其线性部分为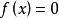 的近似方程,若
的近似方程,若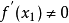 ,则得
,则得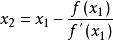 如此继续下去,得到牛顿法的迭代公式:
如此继续下去,得到牛顿法的迭代公式: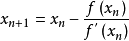 ,通过迭代,这个式子必然在
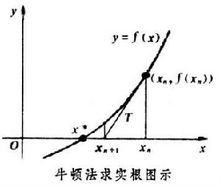
,通过迭代,这个式子必然在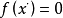 的时候收敛。整个过程如右图:
的时候收敛。整个过程如右图:
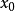 例1 用牛顿法求方程
例1 用牛顿法求方程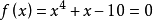 在
在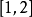 内一个实根,取初始近似值=1.5。 解
内一个实根,取初始近似值=1.5。 解 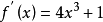 所以迭代公式为:
所以迭代公式为:

列表计算如下:
|| ||
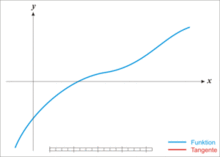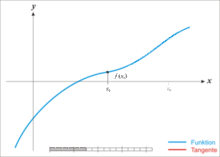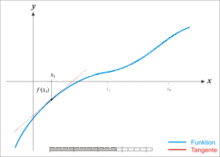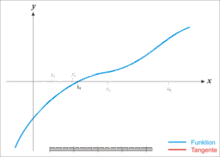
切线法方程f(x)=0的根就是曲线y=f(x)与x轴交点的横坐标x*,当初始近似值x0选取后,过( x0,f(x0))作切线,其切线方程为:y- f(x0)=f′(x0)(x-x0)
一般地,设Xn是x*的第n次近似值,过( x,f(x))作y=f(x)的切线,其切线与x轴交点的横坐标为: 即用切线与x轴交点的横坐标近似代表曲线与x轴交点的横坐标。
牛顿法正因为有此明显的几何意义,所以也叫切线法。
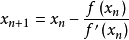
定理设f(x)在[a,b]满足
(1) f(a)·f(b)0, x∈[a,b] 则方程f(x)=0在[a,b]上有且只有一个实根,由牛顿法迭代公式计算得到的近似解序列收敛于方程 f(x)=0 的根 x*。
由方程f(x)=0得到的牛顿迭代形式:
由于f(x*)=0,所以当f′(x*)≠0时, (x* )= 0,牛顿法至少是二阶收敛的,即牛顿法在单根附近至少是二阶收敛的,在重根附近是线性收敛的。
牛顿法收敛很快,而且可求复根,缺点是对重根收敛较慢,要求函数的一阶导数存在。
其它例子第一个例子求方程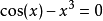 的根。令
的根。令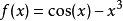 ,两边求导,得
,两边求导,得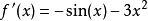 。由于2
。由于2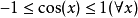 ,则
,则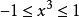 ,即
,即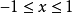 ,可知方程的根位于0和1之间。我们从
,可知方程的根位于0和1之间。我们从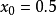 开始。
开始。
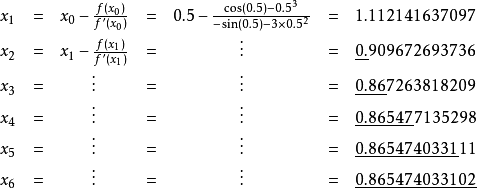
第二个例子牛顿法亦可发挥与泰勒展开式,对于函式展开的功能。
求a的m次方根。
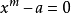
设
而a的m次方根,亦是x的解,
以牛顿法来迭代:
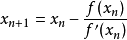
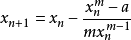
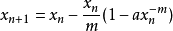
(或 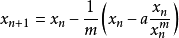 )
)
应用求解最值问题
牛顿法也被用于求函数的最值。由于函数取最值的点处的导数值为零,故可用牛顿法求导函数的零点,其迭代式为
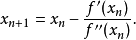




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国