简介
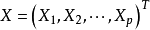 因子分析是简化、分析高维数据的一种统计方法。假定p维随机向量 满足
因子分析是简化、分析高维数据的一种统计方法。假定p维随机向量 满足
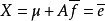
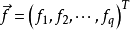 是q维随机变量,
是q维随机变量,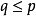 ,满足
,满足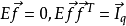 ,它的分量
,它的分量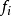 称为公共因子,对X的每个分量都起作用。
称为公共因子,对X的每个分量都起作用。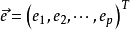 是p维不可观测的随机向量,满足
是p维不可观测的随机向量,满足
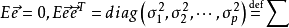
且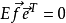 ,e的分量
,e的分量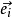 称为特殊因子,它仅对X的分量
称为特殊因子,它仅对X的分量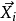 起作用。
起作用。
μ和A为参数矩阵。若X满足上式,则称随机向量X具有因子结构。这时,容易算得
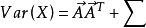 矩阵A称为因子载荷,其元素
矩阵A称为因子载荷,其元素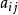 是第i个分量
是第i个分量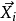 在第j个因子
在第j个因子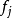 上的载荷。记
上的载荷。记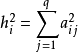 ,则有
,则有
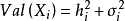 由此可见,
由此可见, 反映了公共因子对
反映了公共因子对 的影响,称为公共因子对
的影响,称为公共因子对 的“贡献”。当
的“贡献”。当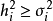 时,表明公共因子对
时,表明公共因子对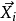 的影响大于特殊因子
的影响大于特殊因子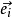 的影响,也可以看出
的影响,也可以看出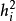 反映了分量
反映了分量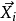 对公共因子
对公共因子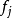 的依赖程度。
的依赖程度。
另一方面,对一个指定的公共因子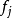 ,记
,记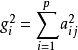 ,称为公共因子
,称为公共因子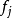 对X的贡献。
对X的贡献。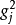 的值越大,反映了公共因子
的值越大,反映了公共因子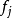 对X的影响也越大,所以
对X的影响也越大,所以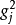 是衡量公共因子重要性的一个尺度。1
是衡量公共因子重要性的一个尺度。1
隐性变量因子分析的主要目的是用来描述隐藏在一组测量到的变量中的一些更基本的,但又无法直接测量到的隐性变量 (latent variable, latent factor)。比如,如果要测量学生的学习积极性(motivation),课堂中的积极参与,作业完成情况,以及课外阅读时间可以用来反应积极性。而学习成绩可以用期中,期末成绩来反应。在这里,学习积极性与学习成绩是无法直接用一个测度(比如一个问题) 测准,它们必须用一组测度方法来测量,然后把测量结果结合起来,才能更准确地把握。换句话说,这些变量无法直接测量。可以直接测量的可能只是它所反映的一个表征(manifest),或者是它的一部分。在这里,表征与部分是两个不同的概念。表征是由这个隐性变量直接决定的。隐性变量是因,而表征是果,比如学习积极性是课堂参与程度 (表征测度)的一个主要决定因素。
因子分析是社会研究的一种有力工具,但不能肯定地说一项研究中含有几个因子,当研究中选择的变量变化时,因子的数量也要变化。此外对每个因子实际含意的解释也不是绝对的。
得到因子因子分析的方法有两类。一类是探索性因子分析法,另一类是验证性因子分析。探索性因子分析不事先假定因子与测度项之间的关系,而让数据“自己说话”。主成分分析和共因子分析是其中的典型方法。验证性因子分析假定因子与测度项的关系是部分知道的,即哪个测度项对应于哪个因子,虽然我们尚且不知道具体的系数。
验证因子探索的因子分析有一些局限性。第一,它假定所有的因子(旋转后) 都会影响测度项。在实际研究中,我们往往会假定一个因子之间没有因果关系,所以可能不会影响另外一个因子的测度项。第二,探索性因子分析假定测度项残差之间是相互独立的。实际上,测度项的残差之间可以因为单一方法偏差、子因子等因素而相关。第三,探索性因子分析强制所有的因子为独立的。这虽然是求解因子个数时不得不采用的机宜之计,却与大部分的研究模型不符。最明显的是,自变量与应变量之间是应该相关的,而不是独立的。这些局限性就要求有一种更加灵活的建模方法,使研究者不但可以更细致地描述测度项与因子之间的关系,而且可以对这个关系直接进行测试。而在探索性因子分析中,一个被测试的模型(比如正交的因子) 往往不是研究者理论中的确切的模型。
分析描述验证性因子分析(confirmatory factor analysis) 的强项正是在于它允许研究者明确描述一个理论模型中的细节。那么一个研究者想描述什么呢?我们曾经提到因为测量误差的存在,研究者需要使用多个测度项。当使用多个测度项之后,我们就有测度项的“质量”问题,即有效性检验。而有效性检验就是要看一个测度项是否与其所设计的因子有显著的载荷,并与其不相干的因子没有显著的载荷。当然,我们可能进一步检验一个测度项工具中是否存在单一方法偏差,一些测度项之间是否存在“子因子”。这些测试都要求研究者明确描述测度项、因子、残差之间的关系。对这种关系的描述又叫测度模型 (measurement model)。对测度模型的质量检验是假设检验之前的必要步骤。
验证性因子分析往往用极大似然估计法求解。它往往与结构方程的方法连用。具体的使用过程与原理可以参看扩展阅读中的《社会调查研究方法》。
因子应用在市场调研中,研究人员关心的是一些研究指标的集成或者组合,这些概念通常是通过等级评分问题来测量的,如利用李克特量表取得的变量。每一个指标的集合(或一组相关联的指标)就是一个因子,指标概念等级得分就是因子得分。
因子分析在市场调研中有着广泛的应用,主要包括:
(1)消费者习惯和态度研究(U&A)
(2) 品牌形象和特性研究
(3)服务质量调查
(4) 个性测试
(5)形象调查
(6) 市场划分识别
(7)顾客、产品和行为分类
在实际应用中,通过因子得分可以得出不同因子的重要性指标,而管理者则可根据这些指标的重要性来决定首先要解决的市场问题或产品问题。
因子分析的任务就是从X的相关矩阵和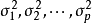 出发,通过方差最大的正交旋转,求出矩阵A的各列,使相应的“贡献”有顺序
出发,通过方差最大的正交旋转,求出矩阵A的各列,使相应的“贡献”有顺序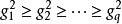




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国