[科普中国]-主理想环

概念定义

一个整环I叫做一个主理想环，假如I的每一个理想都是一个主理想．则称一个主理想环一定是一个唯一分解环．2

等价定义设A为整环，那么下面的条件等价：

1. A是主理想环

2. A的每个素理想都是主理想

4. A的任意理想都是主理想

5. A存在Dedekind–Hasse范数

相关性质定理定理一 主理想环D上的真因子序列1

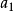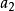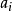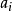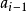， ，…， ，......(其中 是 的真因子)

是一个有限序列。

定理二 主理想环中不可约元生成的理想是极大理想。

定理三 主理想环是唯一分解整环。

定理四 在主理想环D中，设d是a，b的最大公因子，则=。

推论1 在主理想环D中，设d是a，b的最大公因子，则∃u,v∈D使得：au+bv=d。

定理五 （唯一分解性）设R为一主理想环，那么对任意非零元a∈R能够被惟一的分解为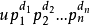 ，这里u 为可逆元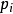， 为所选的素元，并且 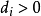。在不考虑置换的条件下，这个分解是唯一的。

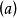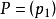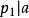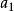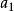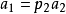**证明：**首先，我们证明分解的存在性。如果a是可逆的，定理平凡成立。否则，令P是包含 的极大理想， 那么有 ，其中 为素元并且 。如果 不可逆，则用 替换a可得 ，其中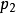 为 素元。重复上面的过程直到 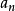可逆为止。如果上面的过程是有限的，那么我们有

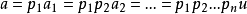，（其中u可逆）。

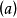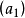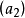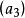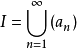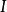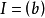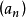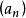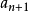否则必存在理想无穷上升链 ⊂ ⊂ ⊂ ⊂ . . . 。令 ，则易知 也为理 想，由R为主理想环知 且b属于某个 ，但这将有 ⊇ 所以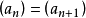 ，此为矛盾！ 所以分解一定是有限的。

唯一性用类似整数分解唯一性的证明方法可得。

举例分析整数环是主理想环，更一般地说，欧几里德环恒为主理想环。

域上的多项式环是主理想环。

高斯整数环是主理想环。

艾森斯坦整数环是主理想环，其中 ω 为任一非 1 的三次单位根。

环 非主理想环：可以证明理想无法由单个元素生成。

例 域F上的一元多项式环F[x]是主理想环。1

证明： 设I是F[x]的任一理想，若I是零理想，则I=。若I不是零理想，则在F[x]中存在次数最低的多项式p(x)，使得⊆I。

对于∀ f(x)∈I，由带余除法知

f(x)=p(x)q(x)+r(x)其中r(x)=0或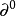 (r(x))