[科普中国]-仿射几何学

简介

平面仿射几何主要研究平面图形在仿射变换下不改变的性质。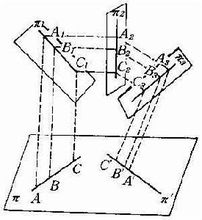

仿射群仿射群是由那些使矩阵为可逆矩阵的映射组成的平面的变换群。这样的变换称为仿射变换。

仿射变换仿射空间中最重要的变换是仿射变换，它的特征是将共线的三点变为共线的三点。给定仿射坐标系后，仿射变换有明确的代数表示。仿射变换全体构成的变换群称为仿射变换群。仿射变换下重要的不变性质和不变量有：共线性、平行性、平行线段的长度比等。

如果在仿射平面（或空间）中引入无穷远点，并且将它们与原有点不加区别，则就成为射影平面（或射影空间）。在射影平面（或射影空间）中指定一条（或一个）直线l（或超平面π），那么射影变换群中保持l（或π）不动的变换就构成一个与仿射变换群同构的变换子群。从这个意义上讲，仿射变换群就是射影变换群的子群，而仿射几何也就成为射影几何的子几何。

平面上的仿射变换可以看成是连续施行有限回两个平面之间的平行投影所得到的平面上点之间的一一对应，也可以说仿射变换是一个平行投影“链”。比如，由连续施行平面π到π1，π1到π2，π2到π3，再从π3回到π的共四次平行投影得到的平面π上点之间的对应，例如A，B，C的对应点为A′，B′，C′，这个对应就是平面π上的一个仿射变换。

平面上的仿射变换由三对不共线的对应点完全确定。线段的长度和二直线的夹角在仿射变换下一般都要改变。但共线三点A，B，C组成的两个有向线段AC和BC的量的比AC/BC（称为A 、B 、C 的简比）在仿射变换下是不改变的，它是仿射变换最基本的不变量。二直线平行这个性质在仿射变换下也不改变。平面上两个封闭图形的面积之比，在仿射变换下也是不变的。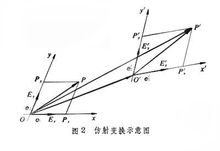

几何特征从几何上来说，可以在空间中取有限多个平面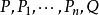,并在每个面上进行平行投射，然后将P和Q上被映射成的点等化便得到了一个仿射变换。1

仿射等价若一个图形经过仿射变换变成另一个图形，就说这两个图形是仿射等价的。

例如：所有的三角形都与正三角形仿射等价，所有的平行四边形都与正方形仿射等价，所有的椭圆都与圆仿射等价，所有的双曲线都与等轴双曲线仿射等价。

在仿射几何中，互相仿射等价的图形是不加区别的。1