[科普中国]-平凡图

定义

平凡图的定义：

1.仅有一个结点的图的称平凡图；

2.平凡图是平凡树；

3.边的集合为空的图叫做零图，1阶零图叫做平凡图，所谓n阶图是指有n个顶点的图；

4.顶点的集合为空的图叫做空图。

图的概念现实世界中许多现象都可以用某种图形表示，这些图形由一些点和连接两点的连线所组成，点表示事物，用点与点之间是否有连线表示事物之间是否有某种联系，这样构成的图形就是图论中的图。2

一个图是一个有序的二元组，记作G，其中

(1)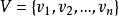是有限非空集合，称为顶点集，其元素称为顶点或结点。

(2)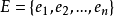是有限集合,称为边集，E中每个元素都有V中的结点对与之对应，称为边。边e既可以是有向的，也可以是无向的。有向边与有序结点对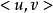对应，这时称u为e的起点，v为e的终点。无向边与无序结点对(u，v)对应，u,v称为e的两个端点。当e为有序对时．图G是有向图：当e为无序对时，图G是无向图。

(3)将图的集合定义转化成图形表示之后，常用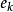表示图的边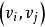．称顶点或边用字母标定的图为标定图，否则称为非标定图。

(4)将有向图各有向边均改成无向边后的无向图称为原有向图的基图。

(5)若一条边连接同一个点，称其为圈或环。

(6)若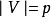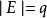，，则通常称它为图G(p,q)。p称为图G的阶。图G(1，0)称为平凡图。边集E为空集的图称为零图。顶点集V和边集E都是有限集的图称为有限图。

(7)若e=(u,v)，则称点u与点v相邻接。并晚点u与边e相关联，点v与边e相关联。若u≠v，则称e与u(或v)的关联次数为1；若u=v，则称e与u的关联次数为2：若u不是e的端点，则称e与u的关联次数为0。同样，若边e和边f有一个共同的端点，则也称边e和边f相邻接。没有边关联于它的顶点称为孤立点，不与其他任何边相邻接的边称为孤立边。2

平凡树平凡图称为平凡树。树是图论中重要内容之一，在计算机科学技术中有着广泛的应用。树的概念由数学家约当(Jordan)给出了统一的定义。一个无圈的连通图称为树，树中点的个数称为该树图的阶，且称次为1的点为悬挂点．与之相邻的边称为悬挂边，仅一个点的图可视为平凡树。

树的定义

连通且无回路的无向图称为无向树，或简称树，常用T表示树。平凡图称为平凡树。无向树中度数为1的顶点称为树叶，度数大于等于2的顶点称为分支点：若无向树T至少有两个连通分支，则称T为森林。

也就是说，(无向)树是连通无回路的简单图，后面提到树时，如果没有特别说明都是指无向树，树的每一条边都是桥。2

相关概念1. 若图G是平凡图或G中任意两点都是连通的，则称图G为连通图，否则称G为非连通图或分离图。

2. 如果图G的顶点集的一个真子集T满足G一T不连通或是平凡图，则称T为G的一个点割(vertex cut)。如果图G的边集的一个真子集S满足G-S不连通或是平凡图，则称S为G的一个边割(edge cut)。3

3. 连通图：如果无向图G中每一对不同的结点x和y间都有一条路(即W((G)=1)，则称G是连通网(connected digraph or graph)．否则称为非连通图(disconnected graph)。3

4. 设G=为无向图，顶点u，v∈V，若u，v之间存在通路，则称顶点u和v是连通的，记作u～v，并规定u与自身是连通的。若无向图G=是平凡图或G中任何两个顶点都是连通的．则称G是连通图，否则，称G为非连通图或分离图。