定义
设f是从A到B的函数,A、B是某线性空间的子集,x₀∈A,对任意x∈A,称x-x₀为自变量在x₀处的增量,记为Δx,相应地,称f(x)-f(x₀)=f(x₀+Δx)-f(x₀)为f在x₀处的增量,记为Δf(x)或Δy(如果函数以y=f(x)表示),增量这个词可理解成增加的量,但可以取负值或0。
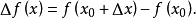
常见函数模型函数类型关于增量,不同的函数有不同的增长特点,自变量变化同样的值对应的增量也是不同的,常见的几类函数模型有
1.一次函数模型: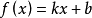 (k,b为常数,k≠0);
(k,b为常数,k≠0);
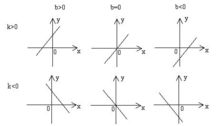
2.反比例函数模型: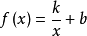 (k,b为常数,k≠o);
(k,b为常数,k≠o);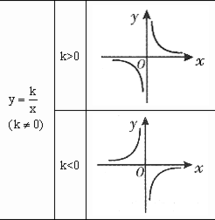
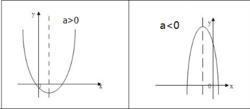
3.二次函数模型: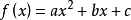 (a,b,c为常数,a≠0);
(a,b,c为常数,a≠0);
4.指数型函数模型: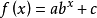 (a,b,c为常数,a≠0,b>0,b≠1;
(a,b,c为常数,a≠0,b>0,b≠1;
5.对数型函数模型: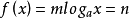 (m,n,a为常数,m≠0,a>0,a≠1);
(m,n,a为常数,m≠0,a>0,a≠1);
6.幂函数模型: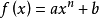 (a,b,n为常数,a≠0,n≠1)1。
(a,b,n为常数,a≠0,n≠1)1。
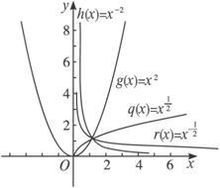
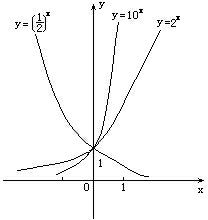
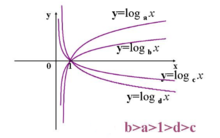
幂函数、对数函数和指数函数的对比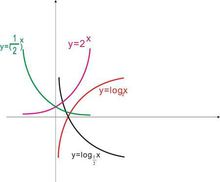
在区间(0,+∞)上,尽管函数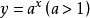 ,
,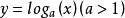 和
和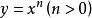 都是增函数,但它们的增长速度不同,而且不在同一个“档次”上。随着x的增大,
都是增函数,但它们的增长速度不同,而且不在同一个“档次”上。随着x的增大,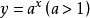 的增长速度越来越快,会超过并远远大于
的增长速度越来越快,会超过并远远大于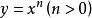 的增长速度,而
的增长速度,而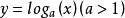 的增长速度则会越来越慢。因此,总会存在一个
的增长速度则会越来越慢。因此,总会存在一个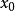 ,当
,当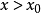 时,就有
时,就有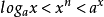 。1
。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国