[科普中国]-约束条件

定义

在优化设计中，目标函数取决于设计变量，而设计变量的取值范围都有各种限制条件，如强度、刚度等。每个限制条件都可写成包含设计变量的函数，称为约束条件或设计约束。因为它是设计变量的函数，也称为约束函数。2

分类约束函数可用等式或不等式描述。如果约束函数能够反映设计变量之间明显的函数关系，称为显式约束；否则，称为隐式约束。2

等式约束是对设计变量的严格约束，起着降低设计自由度的作用，其形式为：

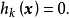式中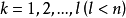． ，l为等式约束的数目，n为设计维数。

在机械优化设计中，大部分约束为不等式约束，其形式为：

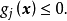式中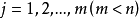， ，m为不等式约束的数目。根据约束的性质，分为几何约束(边界约束)和性能约束。2

几何约束：根据某种设计要求，设计变量必须满足的某些几何条件以及只对设计变量的取值范围加以限制的那些约束，如杆的长度、杆的横截面积等。

性能约束：指满足特定工作性能而建立的约束条件，如工作应力小于许用应力等。

对于等式约束而言，设计变量所代表的设计点必须在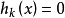 所表示的面(或线)上，称为起作用约束或紧约束。对于不等式约束，极限情况 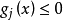所表示的几何面或线将设计空间分成两部分：一部分中所有设计均满足所有的约束条件，这部分空间称为设计点的可行域；另一部分所有点均不满足约束条件，称为设计点的不可行域。在可行域内的设计点，称为可行****设计点，可行域也是可行设计点的集合。位于可行域边界上的设计点亦是可行点，过该点的约束为起作用约束，否则为不起作用约束；非可行域是不满足约束条件设计点的集合。

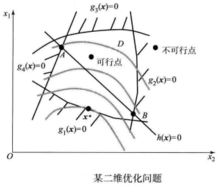
如图1所示的某二维优化设计问题，包含四个不等式约束和一个等式约束。图中分别表示了可行域、不可行域、可行点、不可行点、起作用约束和不起作用约束。2

利用可行域的概念，可以将优化问题的数学模型（见下文）进行简化。设同时满足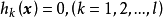和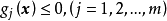 的设计点的集合为D(设计点的可行域)，优化问题的数学模型可简化为：2

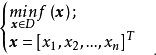
相关概念优化设计数学模型建立优化数学模型，通常是根据设计要求，应用相关基础和专业知识，建立若干个相应的数学表达式。对于机械结构优化设计，主要是根据力学，机械设计等专业基础知识及机械制造等专业知识来建立数学模型。优化问题的一般数学模型如下所示：2

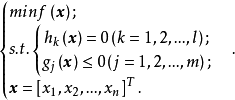
设计变量在设计中不断变化，能够独立影响设计目标的设计参数称为设计变量，一般用列向量或行向量的转置表示。设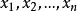 为优化设计中的n个变量，记为2

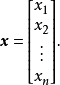或

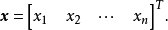
把 定义为门维欧式空间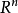 的一个列向量，该空间包含了设计中所有可能的设计方案，且每一个设计方案对应设计空间上的一个设计向量或者一个设计点 。设计变量的个数行称为设计问题的维数，有几个设计变量就称为几维优化设计问题。设计问题的维数表征了设计自由度。自由度越大，越有利于寻找最理想的设计方案，但设计的难度也越大。

n=2就是一个二维设计问题，可以用直角坐标系表示，也称平面设计问题；n=3是一个三维设计问题，可用三个坐标轴所构成的直角坐标系表示，也称三维设计空间；n>3时为抽象的超空间，无法用图形表示。

在设计域中，按变量是否连续分为连续变量(如构件尺寸、转速等)和离散变量(如齿轮的齿数等)。按变量的性质分为几何参数、物理参数和力学参数等，如杆的截面积、长度等即为几何参数，杆的质量、弹性模量和泊松比为物理参数，杆的应力、应变等为力学参数等。

根据设计变量维数的多少，优化设计问题可以分为小型优化设计问题(n50)等2。

目标函数为了对设计进行评价，必须构造包含设计变量的评价函数，即优化的目标，称为目标函数，一般以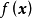 表示。2

在优化过程中，通过设计变量的改变不断改善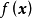 的值，最后求得令 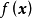值最好或最满意的x值。在目标函数的构造中，应注意目标函数必须包含全部设计变量。

目标函数一般用极小值表示，即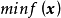 ，若求目标函数的极大值，一般用 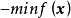转换为极小值问题，因此极大化和极小化都可统一表示为求极小，即

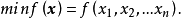
在机械设计中，一般用作目标函数的有体积最小、质量最小、效率最大、柔度最小、振幅或噪声最小、成本最低，等等。

机械优化设计一般分为单目标优化问题和多目标优化问题。只有一个目标函数的优化问题称为单目标优化问题；在同一个设计中要提出多个目标区数时，称为多目标优化问题。目标函数愈多，设计的综合效果愈好，但求解的难度也愈大。

目标函数一般表现为显式和隐式两种。显式目标函数是根据设计理论或公式、科学定理的关系推导的代数方程，或是根据实验数据采用曲线拟合方法所得的曲线方程；隐式目标函数是利用有限元分析方法、人工神经网络方法或仿真模拟方法的程序计算的结果，没有明显的函数式，但可给出函数值。2