概念定义
设D表示一个实数集合(闭区间,开区间,区间的并,集合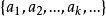 等),设
等),设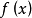 是定义在D上的实值函数,如果存在
是定义在D上的实值函数,如果存在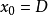 ,使得对D中任何冀
,使得对D中任何冀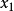 ,
,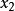 ,当
,当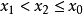 时,有1
时,有1
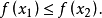
当 时,
时,
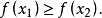
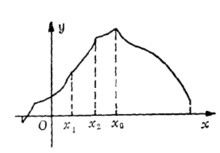
那么就说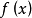 是定义在D上的单峰函数(图1),换句话说,如果
是定义在D上的单峰函数(图1),换句话说,如果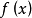 在
在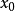 左边递增,在
左边递增,在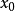 右边递减,那么
右边递减,那么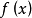 就是D上的单峰函数,
就是D上的单峰函数,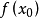 就是
就是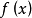 在D上的最大值(峰值)
在D上的最大值(峰值)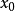 称为峰值点。1
称为峰值点。1
类似.如果存在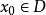 ,使得D中任何
,使得D中任何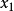 ,
,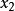 ,当
,当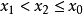 时,有
时,有
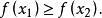
当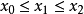 时,有
时,有

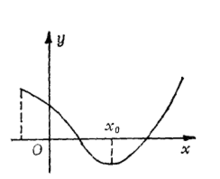
那么就说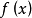 是D上的单谷函数,
是D上的单谷函数,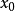 称为谷值点(图2)。
称为谷值点(图2)。
实例分析例1 二次函数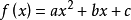 当
当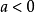 时,为单峰函数,当
时,为单峰函数,当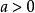 时,为单谷函数。1
时,为单谷函数。1
例2 函数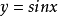 在
在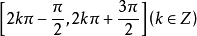 为定数)上为单峰函数,而在
为定数)上为单峰函数,而在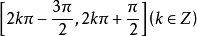 (
(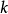 均为定数)上为单谷函数。
均为定数)上为单谷函数。
例3 使用单因素优选法的经验表明,单因素实验指标函数大多为单峰(谷)函数。
例4 函数 ,
,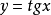 ,
,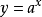 ,
,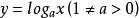 在整个定义域上不是单峰函数,也不是单谷函数。
在整个定义域上不是单峰函数,也不是单谷函数。
由定义可知,单峰函数在定义域上有最大值(峰值),单谷函数有最小值(谷值),这就确定了这函数类在处理极值问题中的地位。
单蜂函数的性质由定义可知,在闭区间或有限集合上的单调函数既为单峰函数,又为单谷函数,这样,就容易证明,对集合D,如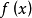 是D上单峰函数,
是D上单峰函数,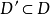 ,则
,则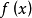 是D'上的单峰函数,对单谷函数也一样,归纳起来,单峰(谷)函数有如下性质。1
是D'上的单峰函数,对单谷函数也一样,归纳起来,单峰(谷)函数有如下性质。1
性质1 单峰函数在其定义域的任何子集上,仍为单峰函数,对单谷函数也一样。
性质2 若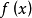 为单峰(谷)函数,那么
为单峰(谷)函数,那么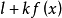 (
(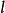 、
、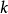 为常数),当
为常数),当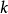 >0时,仍为单峰(谷)函数,当
>0时,仍为单峰(谷)函数,当




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国