[科普中国]-遍历性

定义

设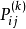 为齐次马氏链 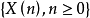的k步转移概率，如果对一切i,j,存在不依赖于i的极限 则称马氏链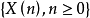 具有遍历性，若 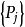构成一个概率分布，则称该马氏链存在着极限分布 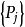。1

遍历定理定理1对于有限状态齐次马氏链，如果存在正整数s,并且对所有的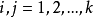 都有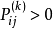成立，则该马氏链必具有遍历性，且式 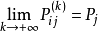中的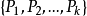 即为极限分布，它的方程组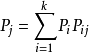满足条件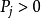 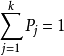， 的唯一解。1

定理2不可约非周期的可列状态其次马氏链存在平稳分布的充要条件是，这个链的所有状态都是正常返的，且这时极限分布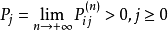是唯一的平稳分布。1

例题分析1．在一计算机系统中，每一循环具有误差的概率取决于先前一个循环是否有误差。以0表示误差状态，以1表示无误差状态，且状态的一步转移概率矩阵为

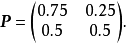试说明相应齐次马尔可夫链是遍历的，并求其平稳分布：

(1)用定义解；

(2)引用遍历性定理解。

解：

（1）因为

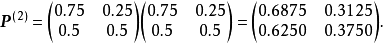
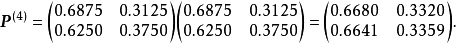
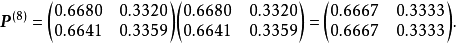
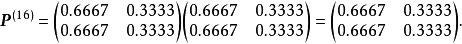
由定义知，此链具有遍历性，其稳态概率为

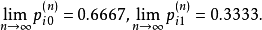（2）由定理知因为的腹元均大于0，故此链具有遍历性，且其稳态概率满足等式

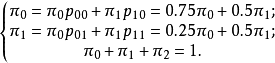解得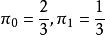 ，即平稳分布 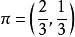。2

2. 设齐次马尔可夫链的一步转移概率矩阵为

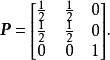证此链不是遍历的。

**解：**因为

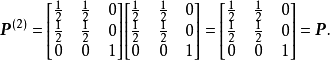
故对于任意的n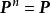， ，且 ，故此链不是遍历的。