[科普中国]-多重图

定义

在无向图中，关联一对顶点的无向边如果多于1条，则称这些边为平行边，平行边的条数称为重数。在有向图中，关联一对顶点的有向边如果多于1条，并且这些边的始点与终点相同(也就是他们的方向相同)，称这些边为平行边。含平行边的图称为多重图，既不含平行边也不含环的图称为简单图。

在图1中，(a)中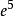 与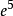 是平行边，在(b)中 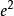与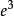 是平行边；注意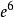， 与 不是平行边。(a)和(b)两个都不是简单图。

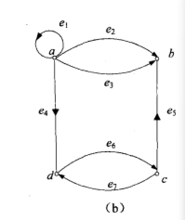
基础概念一个图是一个有序的二元组，记作G，其中1

(1)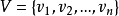 是有限非空集合，称为顶点集，其元素称为顶点或结点。

(2)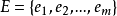 是有限集合，称为边集，E中每个元素都有V中的结点对与之对应，称为边。

边e既可以是有向的，也可以是无向的。有向边与有序结点对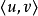 对应，这时称u为e的起点，v为e的终点。无向边与无序结点对 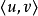对应，u，v称为e的两个端点。

(3)将图的集合定义转化成图形表示之后，常用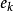 表示图的边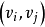 ，称顶点或边用字母标定的图为标定图，否则称为非标定图。

(4)将有向图各有向边均改成无向边后的无向图称为原有向图的基图。

(5)若一条边连接同一个点，称其为圈。

(6)若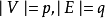 ，则通常称它为 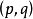图。p称为图G的阶。(1，0)图称为平凡图。边集E为空集的图称为零图。顶点集V和边集E都是有限集的图称为有限图。 、

(7)若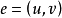 ，则称点u与点v相邻接。并说点u与边e相关联，点v与边e相关联。同样，若边e和边f有一个共同的端点，则也称边e和边f相邻接。没有边关联于它的顶点称为孤立点，不与其他任何边相邻接的边称为孤立边。1

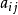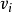多重图的矩阵表示可以用类似于有向图的方法，用矩阵来表示一个多重图，其中每个元素 ，若从 到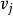 无边相连，则有 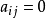；若有边相连，且其重数为k，则 。2

有向多重图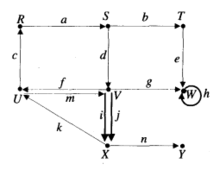

图2中的图形描绘了一个有向多重图(directed multi-graph)。在顶点W上有一个有向环(directed loop)h，从V到X存在平行有向边(parallel directed edges)i和j。因为有向图也是一种特殊的有向多重图，所以在有向多重图上给出的定义也可以应用于有向图。

注意：诸如f和m这样的有向边不是平行有向边，但i和j是平行有向边。3

如果对每个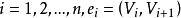 ，则称顶点和有向边的交替序列

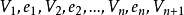为从 到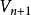 的有向通路(directed path)。这条有向通路的长度为n，即有向边的数目。所以R，a，S，b，T， e，W是一条从R到W长度为3的通路，也可以记作：R，S，T，W或a，b，e。由于从V到X存在两条有向边，有向通路V，i，X，k，U，m，V，j，X不能只用顶点来描述。但是，这条有向通路可以通过仅列出有向边i，k，m，j来描述。此外，T，b，S，d，V不是有向通路，因为有向边b不是从T到S而是从S到T的。同样，不存在从Y出发的长度为正数的有向通路。如前所述，一个顶点是长度为0的有向通路。

有向通路a，d，g是一条从R到W的简单有向通路(simple directed path)。即没有重复顶点的有向通路。有向通路a，d，i，k，m，g不是简单有向通路，这是因为顶点V重复出现了，容易看出每条有向通路都包含一条简单有向通路。

定理 每一条U-V有向通路都包含一条U-V简单有向通路。

图2中的有向通路a，d，f，c是一个有向回路(directed cycle)，因为在这条从P到R的长度为正数的有向通路中不存在其他被访问两次的顶点。但是，b，e，g，d不是有向回路，这是因为有向边g和d的方向不对。h和f，m都可看作有向回路。有向通路k，m，f，c，a，d不是有向回路，这是因为顶点U和V出现了两次。在有向多重图D中，如果对每对顶点A和B都存在一条从A到B的有向通路，那么称D为强连通(strongly connected)的。所以，在一个强连通的有向多重图中，可以沿着有向边，按照某条路线从任何一个顶点出发到达其他任何一个顶点。3