约定记号
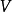 表示一个有穷字母表,
表示一个有穷字母表,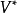 表示由有穷字母表
表示由有穷字母表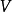 生成的自由半群。
生成的自由半群。
设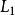 ,
,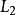 是有穷字母表
是有穷字母表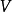 上的两个语言,我们用
上的两个语言,我们用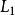
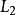 表示
表示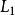 与
与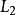 的连接,即
的连接,即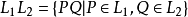 。1
。1
准备概念3型文法或称正则文法,生成式的形式为A→wB或A→w,A,B∈N,w∈T* 称右线性文法;如果生成式的形式为A→Bw或A→w, 则称左线性文法。由正则文法产生的语言称为正则语言。
定义定义1设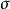 是定义在有穷字母表
是定义在有穷字母表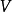 上的一个映射,使得对于任意的
上的一个映射,使得对于任意的 ,
,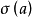 是有穷字母表
是有穷字母表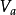 上的一个语言。我们按照如下的规则将映射
上的一个语言。我们按照如下的规则将映射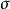 的定义域扩充为
的定义域扩充为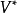 :
:
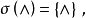
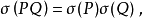 其中
其中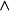 表示空字,P,Q
表示空字,P,Q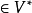 ,称如此得到的由
,称如此得到的由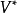 到
到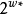 的映射
的映射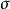 ,其中
,其中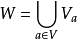 ,是一个置换。1
,是一个置换。1
定义2设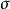 是从有穷字母表
是从有穷字母表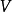 生成的自由半群
生成的自由半群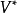 到有穷字母表
到有穷字母表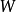 生成的自由半群
生成的自由半群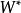 的幂集
的幂集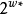 的置换,若对于每个
的置换,若对于每个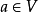 ,均使
,均使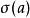 是一个3型语言,则称
是一个3型语言,则称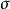 是从
是从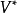 到
到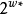 的正则置换。1
的正则置换。1
举例S置换是一类特殊的正则置换。1
S置换定义设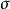 是从有穷字母表
是从有穷字母表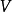 生成的自由半群
生成的自由半群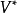 到有穷字母表
到有穷字母表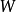 生成的自由半群
生成的自由半群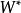 的幂集
的幂集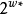 的置换,若
的置换,若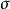 使得集合类
使得集合类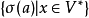 是集合
是集合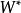 的一个分划,则称置换
的一个分划,则称置换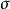 为一个S置换。1
为一个S置换。1
定理1(封闭性)设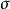 是从有穷字母表
是从有穷字母表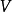 生成的自由半群
生成的自由半群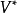 到有穷字母表
到有穷字母表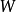 生成的自由半群
生成的自由半群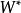 的幂集
的幂集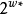 的S置换,若L是
的S置换,若L是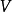 上的一个3型语言,则
上的一个3型语言,则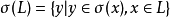 也是3型的。1
也是3型的。1
定理2(充分性)设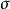 是从有穷字母表
是从有穷字母表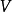 生成的自由半群
生成的自由半群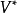 到有穷字母表
到有穷字母表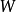 生成的自由半群
生成的自由半群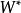 的幂集
的幂集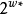 的S置换,则
的S置换,则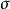 是正则的。1
是正则的。1
正则置换的一种表达式定理:关于V上任何正则置换f,常存在V上的置换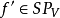 ,使得
,使得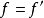 。
。
(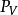 中一切S置换
中一切S置换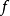 :
: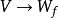 生成的
生成的 子代数记为
子代数记为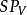 ,其中
,其中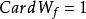 。)2
。)2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国