定义
设x,y是空间X中的两点,如果存在X的连通子集 ,则称点
,则称点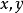 是连通的。1
是连通的。1
①设X为拓扑空间,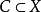 ,若C满足
,若C满足
(1)C是拓扑空间X的连通子集;
(2)C不是拓扑空间X的任意连通子集的真子集。则称C为拓扑空间X的一个连通分支(或极大连通子集)。
②设X是多于一点的拓扑空间,若拓扑空间X的每个单点集都是X的连通分支,则称X为完全不连通空间。2
定理定理1设X为拓扑空间,则
(1)若A是拓扑空间X的连通子集,则存在X的连通分支C,使得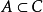 ;
;
(2)拓扑空间X的任意两个不同的连通分支不相交;
(3)拓扑空间X是若干个连通分支的并。
证明 (1)对于拓扑空间X的连通子集A,记
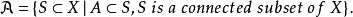
显然,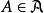 ,从而根据定理可知
,从而根据定理可知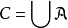 是X的连通子集,并且
是X的连通子集,并且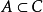 .若有X的连通子集M使得
.若有X的连通子集M使得 ,则
,则 ,于是
,于是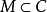 ,因此
,因此 ,所以C是X的极大连通子集,即它是X的连通分支。
,所以C是X的极大连通子集,即它是X的连通分支。
(2)设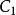 ,
,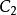 是X的两个不同的连通分支,若
是X的两个不同的连通分支,若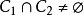 ,则
,则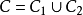 是X的连通子集,从而
是X的连通子集,从而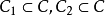 ,所以根据连通分支
,所以根据连通分支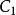 ,
,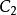 的极大性可知
的极大性可知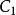 =
=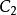 。
。
(3)因为对于任意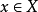 ,
, 是X的连通子集,从而存在连通分支
是X的连通子集,从而存在连通分支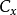 使得
使得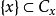 。所以
。所以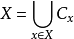 .
.
此定理表明,拓扑空间X的所有连通分支之族是X的一个分类。换言之,X的每个连通分支都是非空集;X的不同连通分支不相交;X的所有连通分支之并为X。2
定理2 拓扑空间的每个连通分支都是闭集。
证明 设C是拓扑空间X的任意连通分支,因为C是X的连通子集,从而 也是X的连通子集,所以由连通分支的极大性可知
也是X的连通子集,所以由连通分支的极大性可知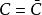 ,即C是闭集。
,即C是闭集。
定理3若C是空间X的连通分支,则C是连通的。1
推论空间X的每个连通分支C都是X的极大连通子集,换言之,C是一个连通集,且不是其它连通集的真子集。
定理4设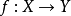 是一同胚映射,
是一同胚映射,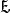 和
和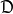 分别是空间X和Y的所有连通分支所成的集,则映射
分别是空间X和Y的所有连通分支所成的集,则映射 是
是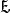 和
和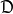 间的一一对应。1
间的一一对应。1
示例例1 多于一点的离散空间是完全不连通空间。
例2 拓扑空间X是连通空间当且仅当X是它的唯一连通分支。2
例3 空间X连通 X是它自己唯一的连通分支.
X是它自己唯一的连通分支.
例4 离散空间X的连通分支恰是它的所有单点集 ,
,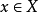
例5 Q作为数直线R的子空间不连通,Q的连通子集也是数直线R的连通子集,从而只能是区间或单点集,但任何区间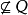 ,故Q的每个连通分支是单点集
,故Q的每个连通分支是单点集 ,x∈Q.这种连通分支均由一个单点组成的空间通常称为完全不连通空间,因单点集
,x∈Q.这种连通分支均由一个单点组成的空间通常称为完全不连通空间,因单点集 不是Q的开集,可见连通分支不必是开集。1
不是Q的开集,可见连通分支不必是开集。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国