[科普中国]-线性独立

基本介绍概念引入

例如，一个运输企业Y有n辆汽车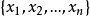，那么Y(在单位时间)的收入(记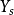为)可表为

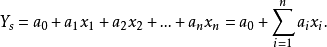
这是个线性函数，其系数表示各自的贡献率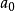，可以为0或负数，比如可表企业的定常支出等。这时则说(企业内)各车之间的关系是线性的。

特别地，所谓“线性关系”的本质就是“独立关系”(又叫线性独立)，因为这时任何一辆车的“贡献”大小和有无(即其系数取正负、大小及是否取0等)皆与别的车无关。1

定义若有m+1个n维不全为零的向量2

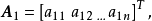
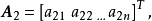
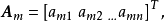
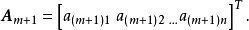如果其中第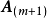个向量可以写成

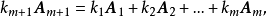这里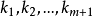为常数，则称这m+1个向量之间存在着线性关系；又称这m+1个向量线性相关；或称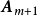是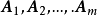的线性表出。当然，由上式可知若这m+1个向量是线性相关的，必可写成

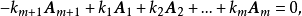这里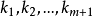必不全为零。

显然，若这m+1个向量不能够写成上面两个式子的形式，或者换个说法只有当的情况下以上两式才成立，则称这m+1个向量是线性独立的。

举例说明例如有以下三个向量

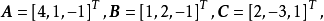它们是线性相关的，因为A可以由B、C线性表出，即 A=2B+C。

若将A向量除去，向量B与向量C则是线性独立的，这是因为B≠kC，k为任意常数．或者说只有才能使得

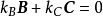成立，所以B与C是线性独立的。2

线性独立与矩阵秩的关系不难证明若有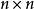阶矩阵

如果它的n个行(列)向量是线性独立的，则该方阵的秩为n，反之如果其n个行向量或n个列向量是线性相关的，则其秩一定小于n，综上所述，可得定理如下：

定理1n×n阶矩阵秩为n的充分必要条件是n个行向量或n个列向量是线性独立的。

让我们以矩阵2

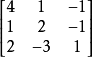为例，对以上定理加以验证．由于该矩阵的三个行向量是线性相关的，故以-2乘第二行向量，以-1乘第三行向量，然后都加到第一行上去，则得到第一行全为零的矩阵

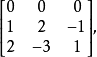故该矩阵的秩小于n，反之，若矩阵的n个行向量或列向量是线性独立的，则无论怎样进行初等变换，也不可能将它变成某一行或某一列为零向量的形式，例如矩阵

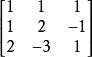就是这样的，该矩阵满秩，秩等于3。

定理2设A为m×n阶矩阵，如果rankA=r，则其m个行向量中有r个是线性独立的，其他(m—r)个行向量可用其线性组合表出。此外n个列向量中也有r个是线性独立的，其它(n-r)个列向量亦可用其线性组合表出。

由此可知，A矩阵的秩的数目就是A矩阵的最大的线性独立的行(列)向量的数目。例如

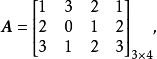因为该矩阵的位于左上角的二阶子行列式

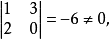而所有3阶子行列式皆等于零，故

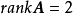则其第一列和第二列是线性独立的，第三列，第四列可以用第一列与第二列线性组合来表示，即2

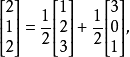
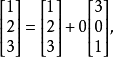
由定理2直接可推断出以下定理。2

定理3设A为m×n阶矩阵，又已知m≤n，如果其中m个行向量是线性独立的，则A矩阵有最大可能的秩，其秩为m。如果n≤m，若其中n个列向量是线性独立的，则A矩阵有最大可能的秩，其秩为n。

如果A矩阵具有最大可能的秩，即rankA=min(m，n)，则称A矩阵为最大秩矩。2