[科普中国]-极限点

关于极限

在点集拓扑学中也有与极限相似的概念，叫做极限点。从字面上看，极限点是极限就要到达的那一点。有时所说极限是数列或函数的极限，是变动的数的极限，极限过程是变量。有时所说极限是点列或映象的极限，是变动的点的极限，极限过程是动点。2

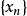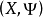度量空间点列的极限定义1设 是度量空间 的无限点列，a是常数，不管给定的正数 多么小，总存在N>0，当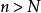 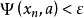， ，则称a是无限点列 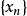的一个极限点。2

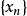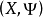定义2设 是度量空间 的无限点列，a是 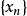的一个极限点。则称无限点列 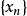收敛于a或极限为a，记为 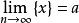。2

例1 无限恒常数列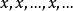 的极限点或极限均是x。

例2设 是离散拓扑空问， ，任意x∈X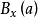， 是含x的开球，若要点列 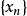收敛于x，则含x的开球必须包含 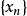几乎所有的项，之后的项均为X，从而 。

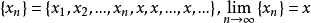注记1：度量空间点列的极限点或极限是唯一的，但在非度量拓扑空间中，极限点或极限就不一定唯一。请看例3。2

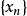例3设 是平凡拓扑空间，任意点x∈X，若 是X中的点列，则因为 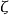中只有一个非空集X，所以包含x的球只有X，从而点列 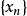收敛于X的任一点x。

极限点的定义定义3设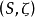 是拓扑空间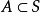，，若对每个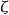 中的集合B，s∈B，有

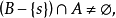则称s是A的一个极限点。2

注记2：定义3是在非度量拓扑空间中极限点的定义，它比定义1和定义2更广泛，一般不具唯一性。

定理1设X是非空集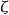， 是平凡拓扑．即 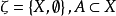，则以下3个结论成立：

(1)若A是空集，则A无极限点；

(2)若A是单点集，其元素为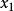 ，则只要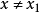 ，x都是A的极限点；

(3)若A至少有2个元素，则A中每一点都是A的极限点。

双核拓扑会计空间的极限点在双核拓扑会计空间中所有的点都不是极限点，原因是以下定理。2

定理2设 是离散拓扑空间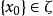， 。则 不可能是任何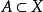 的极限点。

定理3双核拓扑会计空间资产核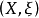 中，若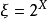 ，则所有资产核纲目都不存在极限点。

证明 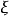是X的所有子集的系，即 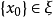，由定理2，任何 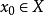不可能是任何纲目 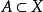的极限点。

定理4双核拓扑会计空间权益核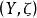 中，若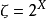 ，则所有权益核纲目都不存在极限点。2

证明 同定理3的证明。

**注记3：**双核拓扑会计空间Z没有极限点，是因为我们为双核会计空间选用了离散拓扑结构，由定理2．任何在单点集 中的点x都不可能是任何Z中的子集的极限点。

**注记4：**若我们为双核会计空间选用平凡拓扑结构，则由定理1，空间每一点都是至少有两个元素的集合的极限点，但是平凡拓扑结构太粗，不适合双核会计空间。2