矩阵的线性运算
矩阵的加法和数乘运算,统称为矩阵的线性运算。1
矩阵加减法定义 设

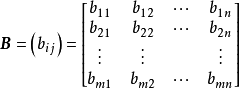 是两个
是两个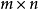 型矩阵,则矩阵
型矩阵,则矩阵
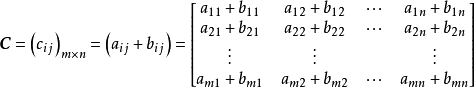 称为
称为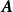 和
和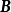 的和,记为
的和,记为
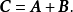
矩阵的加法就是矩阵对应元素相加,当然,相加的矩阵必须要有相同的行数和列数,即只有同型矩阵方可相加。
由于矩阵加法归结为它们元素的加法,即数的加法,故不难验证矩阵加法满足:
(1)结合律: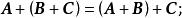
(2)交换律: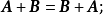
明显地,对零矩阵,有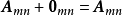 。
。
定义2 矩阵
 称为矩阵
称为矩阵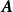 的负矩阵,记为
的负矩阵,记为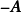 。
。
显然,有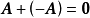 一0,从而可定义矩阵减法为
一0,从而可定义矩阵减法为
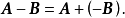
我们可以将负矩阵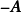 看做是实数一1和矩阵
看做是实数一1和矩阵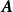 相乘所得,从而抽象出一般数和矩阵的数量乘法。1
相乘所得,从而抽象出一般数和矩阵的数量乘法。1
矩阵数量乘积定义 矩阵
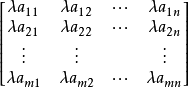 称为矩阵
称为矩阵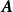 与数
与数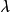 的数量乘积,记为
的数量乘积,记为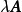 。换句话说,用数
。换句话说,用数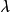 乘以矩阵
乘以矩阵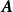 ,就是把矩阵的每个元素都乘上
,就是把矩阵的每个元素都乘上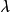 。1
。1
不难验证。数量乘积满足下列运算规律:
(1) (结合律);
(结合律);
(2)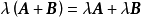 ;
;
(3)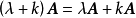 。
。
向量的线性运算向量的加法和数乘运算,统称为向量的线性运算。2
向量的加减法设n维向量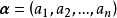 ,
,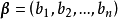 ,规定向量
,规定向量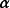 与
与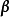 的和为
的和为
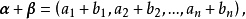 规定向量
规定向量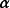 与
与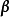 的差为
的差为
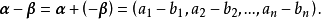
向量的数乘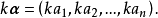
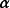 设n维向量
设n维向量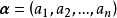 ,各分量乘以数k所构成的向量,称为数k与向量的数量乘积,简称数乘,记做
,各分量乘以数k所构成的向量,称为数k与向量的数量乘积,简称数乘,记做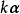 ,即
,即
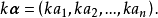
容易验证得到:
(1 )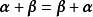 (加法交换律);
(加法交换律);
(2)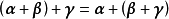 (加法结合律);
(加法结合律);
(3)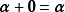 ;
;
(4)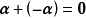 ;
;
(5)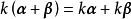 (数乘分配律);
(数乘分配律);
(6)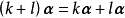 (数乘分配律);
(数乘分配律);
(7) (数乘结合律);
(数乘结合律);
(8) 。
。
上述定义与性质是针对行向量而言的,当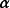 与
与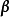 为列向量时,有类似结论。2
为列向量时,有类似结论。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国