基础知识
自然界中的有两类现象,确定性现象和随机现象。
确定性现象:在一定的条件下必然发生(或不发生)某种结果的现象。
例如:太阳从东方升起;水在标准大气压下加温到100℃沸腾。
随机现象:在基本条件不变的条件下,一系列试验(或观察)常会得到不同的结果。
例如:掷一枚硬币,正面朝上或反面朝上;一天内进入某超市的顾客数。
随机现象的统计规律性: 随机现象的各种结果会表现出一定的规律性,这种规律性称之为统计规律性。
随机事件的特征是具有现象的不确定性,但是我们可以通过重复观测,从不确定现象中寻找、观察特定事件发生的规律,为此需要让某一随机现象重复发生(不一定是人为控制的)并记录观测结果,称之为随机试验
随机试验的三个特征:①可以在相同条件下重复进行;②事先知道可能出现的结果;③进行试验前并不知道哪个试验结果会发生。
样本点:随机试验的每一个可能结果。
样本空间:虽然随机事件的结果是不确定的,但结果的范围必须是已知的,可以描述的。把随机试验的每一种可能出现的(不能再分割的)结果称为随即试验的样本点或者基本事件,所有可能结果的集合,也就是样本点的总和称为随机试验的样本空间。样本空间分为三类:离散样本空间、连续样本空间、混合型1。
定义事件域的元素应该包括样本空间和空集;其次应该保证事件经过并、交、差、对立各种运算后仍然是事件,即其对集合的运算有封闭性。(交的运算可以通过并与对立来实现;差的运算可通过对立与交来实现)。
设Ω为样本空间,F 是由Ω的子集组成的集合类,若F满足以下三点:
1.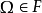 ;2.若
;2.若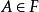 ,则
,则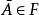 ;3.若
;3.若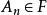 ,n=1,2...,则
,n=1,2...,则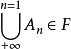 。
。
则称 F 为波雷尔**(****Borel**事件域),或 事件域或
事件域或 代数。波雷尔事件域中每一个样本空间的子集称为一个事件。( Ω,F )为可测空间2。
代数。波雷尔事件域中每一个样本空间的子集称为一个事件。( Ω,F )为可测空间2。
基本类型1.样本空间包含可列(可数)的元素,从而事件域包含可列个事件,生成的概率是离散型概率;
2.样本空间包含不可数的元素,从而事件域包含不可数的事件,生成的概率是连续型概率3。
相关内容样本空间Ω与事件域F是抽象的、理论上是存在的;
事件域 F是集类,随机事件是集合且是 F中的元素;
事件必是样本空间的子集,但样本空间的子集并非是事件;
必然事件与不可能事件也称为随机事件;
事件发生是指当且仅当出现了该事件所含的某一基本事件2。
例子分析例1.掷一枚硬币。
分析:出现“正面”、“反面”都是基本事件。这两个基本事件构成一个样本空间。在例1中共有两个样本点:“正面”,“反面”。作F={正面或反面,正面,反面,空集},它构成一个波雷尔事件域,其中每一个元素都是一个事件。需要说明,F表达式中的花括号。是指事件的集合。
例2.掷一颗骰子。
分析:出现“1点”、“2点”、“3点”、“4点”、“5点”、“6点”都是基本事件。这六个基本事件构成一个样本空间。在例2中共有六个样本点,记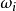 为出现“i点”的样本点,i=1,2,3,4,5,6。作F={
为出现“i点”的样本点,i=1,2,3,4,5,6。作F={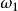 ...
...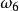 ,(
,( ),
),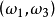 ...
...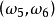 ,
,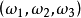 ,
,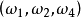 ...
...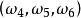 ,
,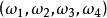 ...
...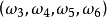 ,
,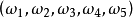 ...
...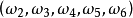 ,
,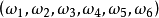 它构成一个波雷尔事件域。这里每一对小括号表示它所包含的样本点的集合。3
它构成一个波雷尔事件域。这里每一对小括号表示它所包含的样本点的集合。3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国