[科普中国]-时间序列分析

基础知识

时间序列是按时间顺序的一组数字序列。

时间序列的特点：

现实的、真实的一组数据，而不是数理统计中做实验得到的。既然是真实的，它就是反映某一现象的统计指标，因而，时间序列背后是某一现象的变化规律。

动态数据。

时间序列建模基本步骤是：

用观测、调查、统计、抽样等方法取得被观测系统时间序列动态数据。

根据动态数据作相关图，进行相关分析，求自相关函数。相关图能显示出变化的趋势和周期，并能发现跳点和拐点。跳点是指与其他数据不一致的观测值。如果跳点是正确的观测值,在建模时应考虑进去，如果是反常现象，则应把跳点调整到期望值。拐点则是指时间序列从上升趋势突然变为下降趋势的点。如果存在拐点，则在建模时必须用不同的模型去分段拟合该时间序列，例如采用门限回归模型。

辨识合适的随机模型，进行曲线拟合，即用通用随机模型去拟合时间序列的观测数据。对于短的或简单的时间序列，可用趋势模型和季节模型加上误差来进行拟合。对于平稳时间序列，可用通用ARMA模型（自回归滑动平均模型）及其特殊情况的自回归模型、滑动平均模型或组合-ARMA模型等来进行拟合。当观测值多于50个时一般都采用ARMA模型。对于非平稳时间序列则要先将观测到的时间序列进行差分运算，化为平稳时间序列，再用适当模型去拟合这个差分序列。

性质特点时间序列分析是定量预测方法之一。它包括一般统计分析(如自相关分析，谱分析等)，统计模型的建立与推断，以及关于时间序列的最优预测、控制与滤波等内容。经典的统计分析都假定数据序列具有独立性，而时间序列分析则侧重研究数据序列的互相依赖关系。后者实际上是对离散指标的随机过程的统计分析，所以又可看作是随机过程统计的一个组成部分。例如，记录了某地区第一个月，第二个月，…，第N个月的降雨量，利用时间序列分析方法，可以对未来各月的雨量进行预报。

基本思想：根据系统的有限长度的运行记录（观察数据），建立能够比较精确地反映序列中所包含的动态依存关系的数学模型，并借以对系统的未来进行预报。

基本原理：一是承认事物发展的延续性。应用过去数据，就能推测事物的发展趋势。二是考虑到事物发展的随机性。任何事物发展都可能受偶然因素影响，为此要利用统计分析中加权平均法对历史数据进行处理。

特点：简单易行，便于掌握，但准确性差，一般只适用于短期预测。

分类时间序列依据其特征，有以下几种表现形式，并产生与之相适应的分析方法：

长期趋势变化：受某种基本因素的影响，数据依时间变化时表现为一种确定倾向，它按某种规则稳步地增长或下降。

使用的分析方法有：移动平均法、指数平滑法、模型拟和法等。

季节性周期变化：受季节更替等因素影响，序列依一固定周期规则性的变化，又称商业循环。

采用的方法：季节指数。

循环变化：周期不固定的波动变化。

随机性变化：由许多不确定因素引起的序列变化。

时间序列分析主要有确定性变化分析和随机性变化分析。其中，确定性变化分析包括趋势变化分析、周期变化分析、 循环变化分析。随机性变化分析：有AR、MA、ARMA模型等1。

具体方法确定性时序分析确定性时序分析的目的：克服其它因素的影响，单纯测度出某一个确定性因素对序列的影响；推断出各种确定性因素彼此之间的相互作用关系及它们对序列的综合影响。

时间序列趋势分析目的：有些时间序列具有非常显著的趋势，我们分析的目的就是要找到序列中的这种趋势，并利用这种趋势对序列的发展作出合理的预测。

常用方法：趋势拟合法和平滑法。

趋势拟合法就是把时间作为自变量，相应的序列观察值作为因变量，建立序列值随时间变化的回归模型的方法。包括线性拟合和非线性拟合。

线性拟合的使用场合为长期趋势呈现出线形特征的场合。参数估计方法为最小二乘估计。

其模型为，，。

非线性拟合的使用场合为长期趋势呈现出非线形特征的场合。其参数估计的思想是把能转换成线性模型的都转换成线性模型，用线性最小二乘法进行参数估计。实在不能转换成线性的，就用迭代法进行参数估计。

其模型有、、等。

平滑法是进行趋势分析和预测时常用的一种方法。它是利用修匀技术，削弱短期随机波动对序列的影响，使序列平滑化，从而显示出长期趋势变化的规律2。

时间序列预测法

时间序列预测法可用于短期预测、中期预测和长期预测。根据对资料分析方法的不同，又可分为：简单序时平均数法、加权序时平均数法。

简单平均数法：也称算术平均法。即把若干历史时期的统计数值作为观察值，求出算术平均数作为下期预测值。这种方法基于下列假设：“过去这样，今后也将这样”，把近期和远期数据等同化和平均化，因此只能适用于事物变化不大的趋势预测。如果事物呈现某种上升或下降的趋势，就不宜采用此法。
加权平均数法：把各个时期的历史数据按近期和远期影响程度进行加权，求出平均值，作为下期预测值3。

随机性变化分析随机时间序列模型（nime series modeling）是指仅用它的过去值及随机扰动项所建立起来的模型，其一般形式为。取线性方程、一期滞后以及白噪声随机扰动项（ ）。

模型将是一个1阶自回归过程AR(1)：。这里，特指一白噪声。

一般的p阶自回归过程AR(p)是。

如果随机扰动项是一个白噪声()，则称(1)式为一纯AR(p)过程（pure AR(p) process），记为。

如果不是一个白噪声，通常认为它是一个q阶的移动平均（moving average）过程MA(q)：。

将纯AR(p)与纯MA(q)结合，得到一个一般的自回归移动平均（aunoregressive moving average）过程ARMA（p，q）：。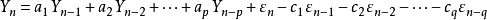

该式表明：
1.一个随机时间序列可以通过一个自回归移动平均过程生成，即该序列可以由其自身的过去或滞后值以及随机扰动项来解释。
2.如果该序列是平稳的，即它的行为并不会随着时间的推移而变化，那么我们就可以通过该序列过去的行为来预测未来。这也正是随机时间序列分析模型的优势所在。需要说明的是，上述ARMA(p，q)模型中均未包含常数项。如果包含常数项，常数项并不影响模型的原有性质，因为通过适当的变形，将包含常数项的模型转换为不含常数项的模型2。

主要用途时间序列分析常用在国民经济宏观控制、区域综合发展规划、企业经营管理、市场潜量预测、气象预报、水文预报、地震前兆预报、农作物病虫灾害预报、环境污染控制、生态平衡、天文学和海洋学等方面。主要包括从以下几个方面入手进行研究分析。

系统描述

根据对系统进行观测得到的时间序列数据，用曲线拟合方法对系统进行客观的描述。

系统分析

当观测值取自两个以上变量时，可用一个时间序列中的变化去说明另一个时间序列中的变化，从而深入了解给定时间序列产生的机理。

预测未来

一般用ARMA模型拟合时间序列，预测该时间序列未来值。

决策和控制

根据时间序列模型可调整输入变量使系统发展过程保持在目标值上，即预测到过程要偏离目标时便可进行必要的控制2。