[科普中国]-振动弛豫

振动弛豫（vibrational relaxation），指的是由于和周围环境碰撞时发生的能量转移，使分子丧失振动激发能的过程。对于大分子，可以不要求以碰撞为前提，弛豫过程可通过分子内各振动模之间的偶合和能量的再分配而实现。

研究背景第一次记录荧光现象的是16世纪西班牙的内科医生和植物学家N.Monardes，他于1575年提到，在含有一种称为“Lignum Ncphriticum”的木头切片的水溶液中，呈现出极为可爱的天蓝色。以后逐步有一些学者也观察和描述过荧光现象，但对其本质及含义的认识都没有明显的进展。

直到1852年，对荧光分析法具有开拓性工作的Stokes在考察奎宁和绿色素的荧光时，用分光计观察到其荧光的波长比入射光的波长稍为长些，而不是由光的漫反射引起的，从而导入荧光是光发射的概念，并提出了 “荧光”这一术语，他还研究了荧光强度与荧光物质浓度之间的关系，并描述了在高浓度或某些外来物质存在时的荧光猝灭现象。可以说，他是第一个提出应用荧光作为分析手段的人。 1867年，Goppelsriide应用铭一桑色素配位化合物的荧光测定铝，这是历史上首次进行的荧光分析工作。1

相关知识荧光是指一种光致发光的冷发光现象。当某种常温物质经某种波长的入射光（通常是紫外线）照射，吸收光能后进入激发态，并且立即被激发并发出比入射光的的波长长的出射光（通常波长在可见光波段）；而且一旦停止入射光，发光现象也随之立即消失。具有这种性质的出射光就被称之为荧光。

分子能级和跃迁分子能级比原子能级复杂；在每个电子能级上，都存在振动，转动能级；

激发：基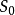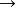态（）激发态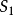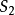（，激发态振动能级）：吸收特定频率的辐射；量子化；跃迁一步到位；

失活：从激发态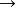基态：速度最快，激发态寿命最短的途径占优势；1

电子激发态的多重度每个分子中都具有一系列严格分立相隔的能级，称为电子能级，而每个电子能级中又包含有一系列的振动能级和转动能级。分子中电子的运动状态除了电子所处的能级外，还包含有电子的多重态，用M=2S+1表示，S为各电子自旋量子数的代数和，其数值为0或1。根据Pauli不相容原理，分子中同一轨道所占据的两个电子必须具有相反的自旋方向，即自旋配对。若分子中所有电子都是自旋配对的，则S=0，M=1，该分子便处于单重态（或叫单重线），用符号S表示。大多数有机化合物分子的基态都处于单重态。基态分子吸收能量后，若电子在跃迁过程中，不发生自旋方向的变化，这时仍然是M=l，分子处于激发的单重态；如果电子在跃迁过程中伴随着自旋方向的变化，这时分子中便具有两个自旋不配对的电子， 即 S=1，M=3，分子处于激发的三重态，用符号T表示。

电 子激发态的多重度：M=2S+1；S为电子自旋量子数的代数和（0或1）；处于分立轨道上的非成对电子 ， 自旋平行要比自旋配对更稳定些（洪特规则），三重态能级比相应单重态能级低 ；大多数有机分子的基态处于单重态；1

跃迁规则Franck-Condon 原理 ：在电子跃迁完成的瞬间 ，分子中原子核构型是来不及改变的 。跃迁前后原子核的构型没有发生改变 、跃迁过程中电子自旋没有改变 、跃迁前后电子的轨道在空间有较大的重叠和轨道的对映性发 生了改变的跃迁是允许的。跃迁过程中电子自旋发生了改变 、跃迁前后电子的轨道在空间不重叠或轨道的对映性未发生改变的跃迁是禁阻的 。

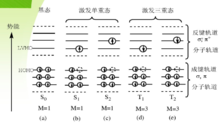
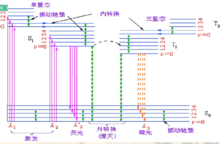
激发态到基态的能量传递途径电子处于激发态是不稳定状态，返回基态时，通过辐射跃迁和无辐射跃迁等方式失去能量。激发态停留时间短，返回速度快的途径，发生的几率大；2

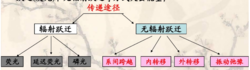
荧光产生过程（1）处于基态最低振动能级的荧光物质分子受到紫外线的照射，吸收了和它所具有的特征频率相一致的光线，跃迁到第一电子激发态的各个振动能级；（2）被激发到第一电子激发态的各个振动能级的分子通过无辐射跃迁降落到第一电子激发态的最低振动能级；（3）降落到第一电子激发态的最低振动能级的分子继续降落到基态的各个不同振动能级，同时发射出相应的光量子，这就是荧光：（4）到达基态的各个不同振动能级的分子再通过无辐射跃迁最后回到基态的最低振动能级。3

振动弛豫的定义振动弛豫（Vibration relaxation）： 当分子吸收光辐射后可能从基态的最低振动能级(v=0)跃迁到激发单重态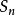的较高振动能级上。然后，在液相或压力足够高的气相中，分子间的碰撞几率很大，分子可能将过剩的振动能量以热的形式传递给周围环境，而自身从激发态的高振动能级跃迁至该电子能级的最低振动能级上，这个过程称为振动弛豫。发生振动他豫的时间为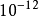数量级。4

实际应用荧光探针

与 蛋白质或其他大分子结构非共价作用而使一种或几种荧光性质发生改变的小分子物质。可用于研究大分子物质的性质和行为。目前常用的荧光探针有荧光素类探针、无机离子荧光探针、荧光量子点、分子信标等。荧光探针除应用于核酸和蛋白质的定量分析外，在核酸染色、DNA电泳、核酸分子杂交、定量PCR技术以及DNA测序上都有着广泛的应用。5

本词条内容贡献者为:

唐浩宇 - 教授 - 湘潭大学