[科普中国]-随机游动

定义

随机游动亦称随机徘徊。一种最基本的整值随机过程。假定一质点在数轴的整点上做如下运动：每次质点以概率 p 向右 1 单位；以概率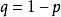向左 1 单位，且各次运动相互独立。以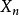表示时刻 n 质点的位置，则过程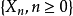称为随机游动，由假设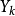表示质点的第 k 次位移，由假设 {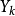} 独立分布：

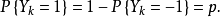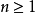而对，有

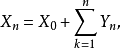于是它是平稳独立增量过程，从而是离散时间时齐马尔可夫链，其一步转移概率为

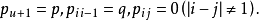
若质点可以在整个数轴的整数点上游动，则称这种随机游动为无限制随机游动。若在某点D设有一个吸收壁，质点到达这点即被吸收而不再游动，因而整个游动也就结束了，这种随机游动称为在D点有吸收壁的随机游动，若P=Q=1/2，随机游动称为对称的。

随机环境中的随机游动[random walk in random environments]

设(V，E)是无穷的有向图，具有可数的顶点集 V 和边集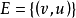。对任意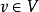，定义它的邻域（neighborhood)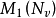，表示支撑为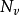的 V 上的概率测度全体。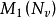中的元素称为在 v 点的转移律（transition law)，是定义在 V 上的可测函数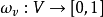满足如下条件：

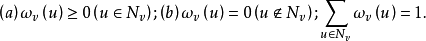
在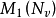上赋予概率测度的弱拓扑使其为波兰空间（Polish space），进而诱导出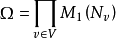上的波兰结构，以F 表示Ω上的博雷尔σ代数。给定（Ω，F）上的一个概率测度P ，一个随机环境（random environment)就是取值在Ω中的一个随机变量ω，其分布为 P。

对任意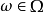，定义随机环境ω中对随机游动（random walk in random environment ω）为取值在 V 中的时齐马尔可夫链，其转移概率为

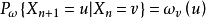
以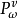表示满足初始条件在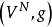上诱导的概率，称为随机游动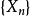的淬火概率（quenched law）。在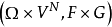上定义为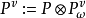

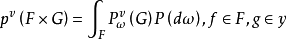
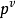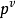在不引起混淆的情况下，也以记在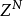上的边际分布，称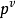为随机游动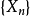的退火概率（annealed law）。1