[科普中国]-优选法

介绍

优选法在数学上就是寻找函数极值的较快较精确的计算方法。1953年美国数学家J.基弗提出单因素优选法枣分数法和0.618法（又称黄金分割法） ，后来又提出抛物线法。至于双因素和多因素优选法，则涉及问题较复杂，方法和思路也较多，常用的有降维法、瞎子爬山法、陡度法、混合法、随机试验法和试验设计法等。优选法的应用范围相当广泛，中国数学家华罗庚在生产企业中推广应用取得了成效。企业在新产品、新工艺研究，仪表、设备调试等方面采用优选法，能以较少的实验次数迅速找到较优方案，在不增加设备、物资、人力和原材料的条件下，缩短工期、提高产量和质量，降低成本等。

优选法,是指研究如何用较少的试验次数，迅速找到最优方案的一种科学方法。例如：在现代体育实践的科学实验中，怎样选取最合适的配方、配比；寻找最好的操作和工艺条件；找出产品的最合理的设计参数，使产品的质量最好，产量最多，或在一定条件下使成本最低，消耗原料最少，生产周期最短等。把这种最合适、最好、最合理的方案，一般总称为最优；把选取最合适的配方、配比，寻找最好的操作和工艺条件，给出产品最合理的设计参数，叫做优选。也就是根据问题的性质在一定条件下选取最优方案。最简单的最优化问题是极值问题，这样问题用微分学的知识即可解决。

实际工作中的优选问题 ，即最优化问题，大体上有两类：一类是求函数的极值；另一类是求泛函的极值。如果目标函数有明显的表达式，一般可用微分法、变分法、极大值原理或动态规划等分析方法求解（间接选优）；如果目标函数的表达式过于复杂或根本没有明显的表达式，则可用数值方法或试验最优化等直接方法求解（直接选优）。

优选法是尽可能少做试验，尽快地找到生产和科研的最优方案的方法,优选法的应用在我国从70年代初开始，首先由我们数学家华罗庚等推广并大量应用,优选法也叫最优化方法。

优点怎样用较少的试验次数，打出最合适的训练量，这就是优选法所要研究的问题。应用这种方法安排试验，在不增加设备、投资、人力和器材的条件下，可以缩短时间、提高质量，达到增强体质．迅速提高运动成绩的目的。

基本步骤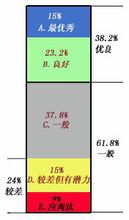1）选定优化判据（试验指标），确定影响因素，优选数据是用来判断优选程度的依据。

2）优化判据与影响因素直接的关系称为目标函数。

3）优化计算。优化(选）试验方法一般分为两类：

分析法：同步试验法

黑箱法：循序试验法

分类优选法分为单因素方法和多因素方法两类。单因素方法1有平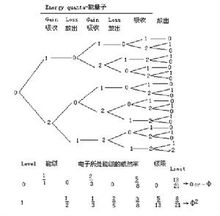分法、0.618法(黄金分割法)、分数法、分批试验法等；多因素方法很多．但在理论上都不完备．主要有降维法、爬山法、单纯形调优胜。随机试验法、试验设计法等。优选法已在体育领域得到广泛应用。

1.单因素优选法

如果在试验时，只考虑一个对目标影响最大的因素，其它因素尽量保持不变，则称为单因素问题。一般步骤：

（1）首先应估计包含最优点的试验范围,如果用a表示下限，b表示上限，试验范围为[a，b];

（2）然后将试验结果和因素取值的关系写成数学表达式,不能写出表达式时，就要确定评定结果好坏的方法。

2.多因素优选法

多因素问题：首先对各个因素进行分析，找出主要因素，略去次要因素，划“多”为“少”，以利于解决问题。

计算方法单因素优选法解决的问题是针对函数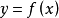 在区间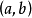 上有单峰极大值（或者极小值），如何通过更加有效的选点方法缩小极值点的范围。

在（a,b）区间内取两点x1，x2。显然：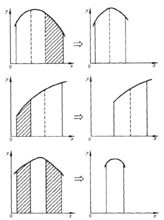

1）当f(x1)>f(x2)时，极大点在（a,x2）的范围内，（x2,b）的区间舍去。

2）当f(x1)eps) B(n)=b(n)-a(n); m(n)=yFunc(t(n)); g(n)=yFunc(u(n)); if m(n)>g(n) a(n+1)=t(n); b(n+1)=b(n); t(n+1)=u(n); u(n+1)=a(n+1)+0.618*(b(n+1)-a(n+1)); else a(n+1)=a(n); b(n+1)=u(n); u(n+1)=t(n); t(n+1)=a(n+1)+0.382*(b(n+1)-a(n+1)); end n=n+1; plot(a(n),yFunc(a(n)),'c*'); plot(b(n),yFunc(b(n)),'b*'); pause(0.5);endxStar = (b(n)+a(n))/2; yStar = yFunc(xStar);plot(a(n),yFunc(a(n)),'ro');hold off;t(n)=0;u(n)=0;m(n)=0;g(n)=0;B(n)=b(n)-a(n);n=n-1; log=[a',b',t',u',m',g',B']; function y = yFunc(x) if (length(x)>1) y = x.^2+5.*x;else y = x^2+5*x;end

对应的Fibonacci法的代码如下：

function [yStar,xStar,log]=FibonacciSearch(a,b,xStep,eps)%% Fibonacci法% 函数：yFunc为y关于x的函数，具体形式见最下，此时为：y=x^2+5*x% 输入：a,b,eps分别代表了区间[-4,4]及精度；xStep为Fibonacci序列划分区间的精度% 输出：[yStar,xStar] 分别是函数的最小值及其对应的x值，log纪录了具体步骤；% 执行：在命令行中输入[yStar,xStar,log]=FibonacciSearch(-4,4,0.2,0.01),% 即可开始在区间[-4,4]中查找最小值，优化精度达到0.01时停止；%figure(1);x = a:0.01:b;y = yFunc(x);plot(x,y,'k-');hold on; n=1;j=1;a(n)=a;b(n)=b;while(Fibonacci(j)*xStepU(n) a(n+1)=r(n); b(n+1)=b(n); r(n+1)=u(n); u(n+1)=a(n+1)+Fibonacci(j-n-1)/Fibonacci(j-n)*(b(n+1)-a(n+1)); else a(n+1)=a(n); b(n+1)=u(n); u(n+1)=r(n); r(n+1)=a(n+1)+(1-Fibonacci(j-n-1)/Fibonacci(j-n))*(b(n+1)-a(n+1)); end plot(a(n),yFunc(a(n)),'c*'); plot(b(n),yFunc(b(n)),'b*'); pause(0.5);endR(j-1)=yFunc(r(j-1));U(j-1)=yFunc(u(j-1));r(j)=r(j-1);u(j)=r(j-1)+eps;R(j)=yFunc(r(j));U(j)=yFunc(u(j));if R(j)>U(j) a(j)=r(j); b(j)=b(j-1);else a(j)=a(j-1); b(j)=u(j);endZ(j-1)=b(j-1)-a(j-1);Z(j)=b(j)-a(j);x=(a(j)+b(j))/2;xStar = (b(n)+a(n))/2; yStar = yFunc(xStar);plot(a(n),yFunc(a(n)),'ro');hold off;log=[a',b',r',u',R',U',Z']; function y = yFunc(x) if (length(x)>1) y = x.^2+5.*x;else y = x^2+5*x;end function F=Fibonacci(n)i=1;Fibonacci(2)=2;Fibonacci(1)=1;if n==0 F=1;else for i=3:1:n Fibonacci(i)=Fibonacci(i-1)+Fibonacci(i-2); end i=n;endF=Fibonacci(i);