[科普中国]-卵形曲线

基本曲线（卵形曲线背景）

如图1所示，为一典型的基本曲线。规定，凡是缓和曲线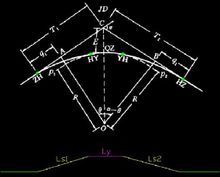的一个端点的曲率为 0（半径无穷大）的，不论长短，以及另一端曲率大小，都称为完整缓和曲线。

基本型曲线的特点是：它由三个曲线元素组成：第一缓和曲线 +圆曲线 +第二缓和曲线，用符号表达，就是： Ls1+Ly+Ls2 ，其中最关键的一点是关于缓和曲线的，不论是 Ls1 还是 Ls2，都必须是完整缓和曲线，它连接直线和圆曲线，其中连接直线的那一端的曲率即为 0。

基本型曲线是各种等级公路主线使用最多的线型， 因此它的计算是最基本的要求。凡是满足基本型曲线的定义的， 其曲线要素、 中桩坐标等均可使用同一套公式进行计算。

基本型曲线可以衍生出以下各种类型的曲线（图2）：

（1）纯圆曲线： Ls1=Ls2=0

（2）对称基本型曲线： Ls1=Ls2

（3）凸形曲线： Ly=0

（4）一侧带缓和曲线： Ls1=0，或者 Ls2=0

以上曲线的计算均可按基本型曲线公式计算。 也就是说，要使用基本型曲线公式计算，要么不带缓和曲线，如果要带，必须是 完整缓和曲线 。

两个基本型曲线直接相连的复曲线，均可按独立的两个基本型曲线进行计算，其中，两个同转向的基本型曲线直接连接的称为 C 型曲线，而两个相反转向的基本型曲线直接连接的称为 S 型曲线。

S 型曲线在各种公路的平面线型中经常使用，而 C 型曲线则很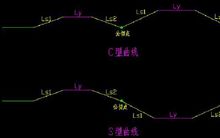少有使用的，究其原因， 是因为其线型不好， 仔细看一看吧， 两曲率不相同的圆曲线之间缓和曲线的连接不合理。那如何解决呢，这就是卵形曲线了。

卵形曲线的定义卵形曲线(见图3)是指在两个同向圆曲线径向衔接或插入的直线长度不足时，用一条回旋线连接两个圆曲线的组合曲线1。它是按直线-缓和曲线 -圆曲线-缓和曲线-圆曲线 -缓和曲线-直线顺序组织构成的几何线形。圆曲线( R1)和( R2)之间的缓和曲线曲率变化范围为1/R1～1/R2。在几何理论上，若两圆曲线相交、相切或相离时，只用一条回旋线不能将两个圆曲线连接起来，所以卵形曲线必须要求大圆曲线能完全包住小圆曲线（假定R1>R2）。并且，为了避免中间缓和段过长或曲率变化过急，一般要求R2/R1=0.2～0.8；缓和曲线的参数C取值范围为 2。

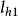卵形曲线的图式如图4所示，CABD为卵形曲线中圆曲线( R1) -缓和曲线-圆曲线( R2)段(为作图方便，省去两端的直线-缓和曲线)。MAB为中间段缓和曲线的补全图。需指出的是，中间段缓和曲线的长度 由f( R1， ，R2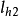， )来决定，且由几何条件得出2：

与C形曲线比较从组合形式看，卵形曲线是由基本型单曲线(见图5)衍生而成的，只是实际运用中，基本型单曲线运用较多，而卵形曲线受地形、地物和其他特殊条件限制，运用频率较少。同样，C形曲线(见图6)也是基本型单曲线衍生而成的。c形曲线定义为同向曲线的两回旋线在曲率为零处径向衔接的形式。C形曲线连接处的曲率为0，相当于两同向曲线中间直线长度为0，对行车和线形都有一定的影响，所以C形曲线在路段上只有在特殊地形下方可使用。

和C形曲线相比，卵形曲线也是同向的、两个不同半径的圆曲线相连的一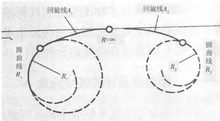种形式，而卵形曲线的特点在于，在两个不同曲率半径(分别是R，、R2)的圆曲线之间，用一条回旋线A进行过渡，而回旋线A的曲率半径则是从R，过渡到R：，这样，卵形曲线的两圆曲线之间的过渡方式比C形曲线要好。在道路路线设计中，鉴于卵形曲线过渡方式好于C形曲线，行驶舒适度也优于C形曲线，故实际设计中，在受地形、地物或其他特殊条件限制时，同向曲线应尽量避免C形曲线的出现，尽量用卵形曲线来调整整体道路中心线的线形设计1。

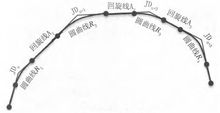
卵形曲线形式常用的卵形曲线也有多种形式，用一个回旋线连接两个同向圆曲线的组合线形叫双心卵形曲线。双心卵形曲线其实就是最基本的卵形曲线(见图3)。在双心卵形曲线基础上，再连接第三个同向圆曲线的组合线形，叫三心卵形曲线(见图7)。在三心卵形曲线的基础上，再接第四个同向圆曲线的组合线形，叫四心卵形曲线(见图8)。理想情况下，无论是多少个圆曲线用回旋线径向连接，其回旋线参数及半径大小均宜在道路相关设计规范限制范围内1。

卵形曲线的判别判别是否是卵形曲线的条件：

（1）两交点必须是相同转向，且两交点曲线之间的直线距离为 0；

（2）两交点中，必定有一个交点的缓和曲线为 0，而且该缓和曲线的位置与另一个交点相接；

（3）由于卵形曲线是两交点、五线元（ Ls1+Ly1+Lf+Ly2+Ls2 ），因此，撇去 QZ 点，两交点总共只有五个主点桩号，直曲表中必有一栏 ZH 点或 HZ 点为空（对应着缓和曲线为 0）；

（4）对于纬地软件生成的直曲表 （类型如宜章至凤头岭高速公路直曲表），两交点半径栏中有一个交点会注明有两个半径值，其中大半径和与之相连的 JD的半径值相等；

（5）最后一条，这一条也是必要条件，就是对于其中一个类似于不对称基本型曲线的交点（如广元至巴中高速公路的 YJD135），假若按基本型曲线计算其曲线要素，与直曲表所列曲线要素绝对不相等。